CINEMATICA, MRUV c3FIS 20, practica online de fisica

home

más de cinemática

otros temas de Física

lecciones del maestro Ciruela

tonterías

NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)

manolito

Fc3.20 - Un globo de gas asciende verticalmente con velocidad constante de 10 m/s. Cuando se encuentra a 16 m del piso, un muchacho que está debajo le dispara con su gomera una piedra, la que parte verticalmente a 30 m/s desde una altura de 1 m.
¿A qué distancia del piso alcanzará la piedra al globo? ¿Cuánto tiempo después de partir? ¿Cuál será la velocidad de la piedra (respecto a la Tierra) en ese instante? Trazar los gráficos correspondientes.

De todas las herramientas cinemáticas, el esquema es la más idónea para organizar la información, para dar la idea general del movimiento con un solo golpe de vista. Aquí va.

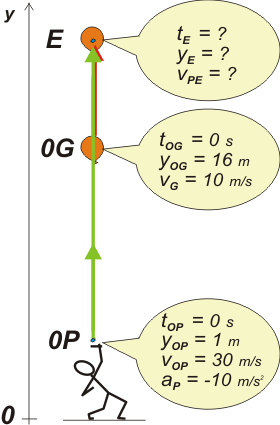
	Observemos detenidamente el esquema. Puse el cero de las alturas en el piso, ya que el enunciado del problema refiere todas las alturas (datos e incógnitas) desde el piso, ¿por qué llevarle la contra? Marqué tres puntos notables: 0P es el evento en el que parte la piedra. 0G es el evento en el que el globo se encuentra a 16 m de altura. (Ya puede verse que los eventos 0P y 0G son simultáneos). Y E el evento en el que la piedra alcanza al globo. Después veremos que la piedra se cruza con el globo en dos oportunidades, pero bueno, nosotros no teníamos por qué apiolarnos de eso de antemano, ni tampoco es necesario. Además el enunciado pregunta sólo por el primer encuentro. Y además seguro que la piedra pincha al globo.
Ahora escribimos las ecuaciones horarias que describen el problema... ¿Cuántas son? Tres, porsupu, porque el globo se mueve con MRU (se describe con una ecuación) y la piedra con un MRUV (dos). Con los modelos a mano:
y = y_o + v ( t – t_o ) y = y_o + v_o ( t – t_o ) + ½ g ( t – t_o )² *v = v_o + g ( t – t_o )*		Modelos.
Para armar las ecuaciones que describen los movimientos de nuestro problema reemplazamos las constantes (t_o, y_o, v_o y a) por las constantes iniciales de cada uno: para la piedra las del punto 0P, para el globo las del punto 0G.


globo	y = 16 m + 10 m/s . t			Estas son las ecuaciones que describen TODO el fenómeno del movimiento contado en el enunciado.
piedra	*y = 1 m + 30 m/s . t* – 5 m/s² . t²**
	*v = 30 m/s – 10 m/s² . t*
Y les pedimos que hablen del punto E. Ellas dicen...
	y_E= 16 m + 10 m/s . t_E		[1]	Estas, en cambio, son las ecuaciones especializadas para los instantes que a vos te interesan.
	*y_E= 1 m + 30 m/s . t_E* – 5 m/s² . t_E²		[2]
	v_p_E = 30 m/s – 10 m/s² . t_E		[3]
¡Oh! ¡Albricias! Hemos encontrado (y no de casualidad, es algo casi inevitable) un sistema de tantas ecuaciones como incógnitas (3x3) donde las incógnitas son aquellas que pregunta el enunciado del problema (miralas bien). Pues... la física del problema ha concluido, el resto es fundamentalmente álgebra, es menos dramático. (Este material me parece un poco reiterativo, todos los problemas me parecen iguales... ¿Por qué no usás algo más divertido?) Aquí una de las 254.328 resoluciones posibles: igualo los segundos miembros de [1] y [2]
	16 m + 10 m/s . t_E= *1 m + 30 m/s . t_E* – 5 m/s² . t_E²
esto es una única ecuación con una única incógnita, t_E. Lo siento, pero t_E está al cuadrado, vas a tener que operar para igualarla a 0 y usar la fórmula salvadora.
	0 = 15 m – 20 m/s . t_E+ 5 m/s² . t_E²

Y obtenemos dos valores de t_e, uno usando el "+" y otro usando el "–". ¿Los dos sirven? ¡Sí!, la piedra alcanza al globo, y si no lo pincha lo sobrepasa. Pero después se va frenando y regresa... y se vuelven a encontrar:
	t_E1= 1 s	t_E₂ = 3 s
Con estos valores voy a las ecuaciones [1] y [2] (en ambas debo obtener los mismos resultados) y así obtengo las alturas en las que piedra y globo se encuentran
	y_E₁= 26 m	y_E₂= 46 m
También los llevo a la ecuación [3] y obtengo la velocidad de la piedra en los cruces
	v_{P_E₁}= 20 m/s	v_{P_E₂}= 0 m/s
Este último resultado es pura casualidad. Significa que el globo alcanza a la piedra justo cuando ésta está por comenzar a bajar. Se hallaba en su altura máxima.

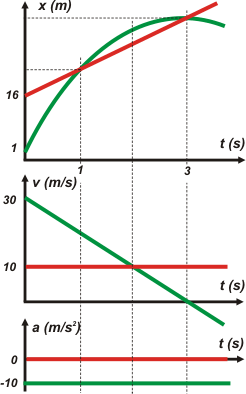
Los gráficos tal vez te sirvan para terminar de cerrar las ideas. Siempre hay que hacerlos en tándem. Acá tenés la piedra en verde y el globo en rojo.

En el gráfico de velocidad en función del tiempo hay dos puntos notables, ¿te animás a encontrarlos, a decir qué significan y a decir si coinciden o no con la información que da el gráfico de alturas?

También tenés que encontrar en el gráfico de velocidad (sólo para practicar) dos áreas iguales. Si te acordás cuál es el significado de las áreas de los gráficos v-t vas a ir al gráfico de y-t para saber qué buscar... y lo vas a encontrar.

DESAFIO: Reescribir el enunciado del problema pero eligiendo un valor para la velocidad de la piedra tal que se encuentre con el globo una sola vez. (No vale pinchar el globo).

Prohibida la reproducción total o parcial de este material didáctico extraordinario por cualquier medio visual, gráfico, sonoro u holográfico sin la correspondiente cita de fuente y autor. Las transgresiones a esta disposición serán penalizadas con la lectura íntegra de "La interpretación de los sueños" de Sigmund Freud. Última actualización ago-06. Buenos Aires, Argentina.