 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
 |
Fc2.06B - Un ciclista que viaja en una trayectoria
rectilínea recorre la mitad de su camino a 30 km/h, y la otra mitad a 20 km/h. Despreciando
el tiempo empleado en variar la velocidad: |
a - Estimar entre qué valores estará el de la velocidad
media con que hizo el viaje.
b - Trazar los gráficos cualitativos de posición
y velocidad en función del tiempo.
c - Calcular el valor de dicha velocidad media.
ADVERTENCIA: vm ≠ (v1+v2)/2. |
|
 |
|
|
¡ A C E R T A S T E !
(Te ganaste una estadía paga en una plaza de Berlín). |
|
|
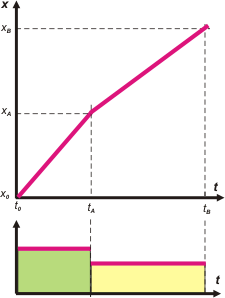 |
Sí, claro que eran ésos. Se puede apreciar que los desplazamientos hechos a cada una de las velocidades son iguales, son las dos mitades (iguales) del camino, tal como indica el enunciado. También se ve claramente que tarda más en recorrer la segunda mitad (que realizó a velocidad menor).
Acá tenés una copia del gráfico posición tiempo correcto, que aproveché para agregarle un poco de información que me va a ser útil, como los nombres de las posiciones e instantes de tiempo en el movimiento del ciclista. |
|
|
|
|
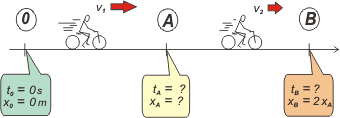
| Como siempre, voy a resolver el ejercicio empezando por un esquema |
|
|
 |
|
|
Un buen número de estudiantes resuelve este problema inventando un valor para el camino total, por ejemplo 100 km y, lógicamente, cada tramo tiene 50 km. Hacer eso es absolutamente innecesario. Y está mal. Al final te explico por qué esta mal. Yo en cambio no sé cuánto vale el camino pero sé que es ( xB – x0 ), y como elijo x0 = 0, el camino es directamente igual a xB. De la misma manera, el primer tramo será igual a xA , y finalmente xB = 2 xA, que es lo que puse en el esquema.
Tenés que tener a mano el modelo de ecuación horaria (MRU):
x = xo + v ( t – to )
Y teniendo el modelo a la vista reemplazamos las constantes para obtener las ecuaciones que describen el movimiento de nuestro ciclista. Con las constantes del globito verde armás la ecuación del primer tramo; y con las constantes del globito amarillo, la ecuación del segundo tramo. Quedan así, fijate:
primer tramo → x = v1 t
segundo tramo → x = xA + v2 ( t – tA )
|
|
Estas son las ecuaciones que describen TODO el movimiento descripto en el enunciado. |
Ahora les pido a las ecuaciones que hablen, a la del primer tramo de pido que hable del punto A; y a la del segundo tramo, que hable del punto B. |
|
|
primera habla de A → xA = v1 tA [1]
segunda habla de B → xB = 2 xA = xA + v2 ( tB – tA ) [2]
|
|
Estas dos hablan sólo de los puntos, que a vos te interesan. |
El resto -como siempre- es álgebra. En nuestro caso tenemos que encontrar un resultado para la velocidad media total del camino... los dos tramos juntos, o sea
vm = ( xB – x0 ) / ( tB – t0 ) = xB / tB
vm = 2 xA / tB [3]
y ese resultado debe ser una expresión en función de v1, v2, y ninguna otra variable más. O sea, los únicos dos datos del problema. Es un álgebra terriblemente complicada. No es más que suma, resta, multiplicación y división... las cuatro operaciones de la primaria. Pero es tediosa y en los 327.852 caminos posibles para llegar al resultado hay muchos estudiantes que se pierden. Te lo recomiendo como ejercicio de álgebra, que seguramente no te viene mal. Probá media hora... hasta cuarenta minutos, dale. Después, si querés volvés y mirás la resolución que hice yo.
De la [2] despejo tB
xA / v2 = ( tB – tA )
tB = ( xA / v2 ) + tA
De la [1] despejo tA y lo meto en la anterior |
|
|
|
|
|
| |
|
|
| Eso es una suma de fracciones. Te acordás cómo se hacía... denominador común... |
|
|
| |
|
|
| tB = |
|
xA v1 + xA v2 |
= |
xA ( v1 + v2 ) |
|
|
|
| v1 v2 |
v1 v2 |
|
|
|
| Esto lo meto en la expresión de velocidad media total, la versión que está en [3] |
|
|
vm = |
|
2 xA |
|
|
| |
xA ( v1 + v2 )
|
|
| v1 v2 |
|
|
|
| Se simplifica xA ; y v1 v2 que esta dividiendo en el denominador, pasa multiplicando en el numerador. |
|
|
| vm= |
|
2 v1 v2 |
FÓRMULA COMPLEMENTARIA 365* |
|
| ( v1 + v2 ) |
|
|
|
| |
|
|
¿Viste que no necesité asignarle un valor al camino total? ¿Es que con letras te resulta más difícil que con números? Si pudiste hacerlo inventando un valor para el recorrido total... te propongo que rehagas el problema exactamente como vos lo resolviste, pero reemplazando el valor que vos pusiste por la letra D. Claro, si en algún momento usaste un número como la mitad del primero... poné D/2; o si usaste un número doble, poné 2D, y así... Al final de cuentas vas a ver que llegás al mismo resultado... ¡y sin inventar ningún valor arbitrario!
Hay muchos profesores que toleran ese tipo de resoluciones "con inventos" en los principiantes (yo uno de ellos), pero en esos desarrollos uno no sabe si arribó a un resultado general o si, por el contrario, llegó a un resultado que depende del invento que hiciste. Por ejemplo: Demostrar que el cuadrado de un número es igual al duplo de ese mismo número... Uy qué difícil... Sea ese número el 2... ¡Verdadero! (Cuando en realidad sabemos que es falso... sólo se verifica para un sólo número, el 2). Bueno, me fui de mambo. |
|
|
| * Anotate esta fórmula complementaria en tu machete. Con ella es probable que resuelvas ejercicios muy rápidamente y sin tanto esfuerzo. Y además es seguro que nunca vas a aprender Física. Ji-ji-jo-ju-ja |
|
|
|
| DESAFIO: En el mismo gráfico posición-tiempo que representa este problema, representar otro ciclista que parte de la misma posición y del mismo instante pero que viaja todo el tiempo a la velocidad media del nuestro. Y en el de abajo, el de velocidad-tiempo, analizá qué son esas dos áreas que te pinté de verde y amarillo, y decime qué relación hay entre ellas. |
|
 |
| |
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima, hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severas. Se permite su reproducción citando la fuente. Última actualización jul-07. Buenos Aires, Argentina. |
|
|
| |
|

