NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniforme)
|
|

|
FIS c2.01- En cada uno de los gráficos se encuentra
representado el movimiento de dos móviles en
colores negro y gris.
Para los cinco primeros escribir las ecuaciones
de movimiento, dar en cada caso las condiciones
iniciales, y si corresponde, determinar cuándo se
produce el encuentro.
En el sexto gráfico decir si pueden escribir las
ecuaciones de posición en función del tiempo
para ambos móviles, ¿se necesita algún dato adicional?,
¿se puede saber dónde se encuentran? |
|
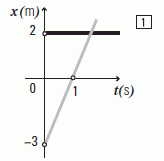 |
Empecemos con el 1. La consigna es armar las ecuaciones horarias. La traza negra describe un móvil que no cambia su posición, está clavado en 2 m. Su ecuación es ésta:
x = 2 m
El que está en gris es un MRU clásico. El modelo de ecuación es éste:
x = xo + v ( t – to )
|
|
|
|
Para armarla tenemos que buscar las tres constantes: to, xo y v. ¿Nos da el gráfico esa información? A ver si nos ponemos de acuerdo en qué información nos da el gráfico exactamente. Volquémosla a una tabla de valores.
|
|
|
|
Para hallar v usaremos el concepto de velocidad media, ya que para el MRU velocidad y velocidad media coinciden perfectamente: v = vm = ΔX / Δt. Esto implica que tenemos que tener un desplazamiento y el intervalo de tiempo correspondiente. Justo lo que tenemos. |
|
|
|
ΔX = 0 m – (– 3) m = 3 m
Δt = 1 s – 0 s = 1 s
|
|
|
|
|
|
v = vm = 3 m/s
¿Quiénes serán to y xo?, parecen ser 0 s y –3m. Pero también podrían ser 1 s y 0 m. Cualquier par es igualmente válido. Dejemos la terna to = 0 s, xo = -3 m y v = 3 m/s |
|
|
x = –3 m + 3 m/s . t |
|
|
Donde se cruzan las rectas es porque ambos móviles se halla en la misma posición en el mismo instante. O sea, un encuentro. Vamos a hallarlo analíticamente. Para eso le pedimos a las ecuaciones de ambos móviles que hablen del encuentro:
xE = 2 m
xE = –3 m + 3 m/s . tE
Y resolvemos algebraicamente como a vos te guste. En este caso obtenemos: |
|
|
| |
xE = 2 m; tE = 1,67 s |
[1] |
|
|
|
| Vamos al segundo caso, que es muy intresante. |
|
|
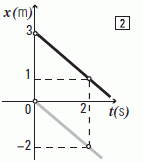 |
Tengamos el modelo a mano:
x = xo + v ( t – to )
La gráfica negra:
x = 3 m – 1 m/s t
La gráfica gris:
x = – 1 m/s t
|
|
|
|
Como ves las dos rectas son paralelas, y como recordás, las paralelas no se cortan. Eso quiere decir que los móviles no se encuentran (y van a estar permanentmente separados por 3 metros). Si se lo quisierasprefuntar a las ecuaciones fijate lo que dirían:
3 m – 1 m/s tE = – 1 m/s tE
Loco, ¿no? Es el modo que tienen las ecuaciones de decirte que no le preguntes por cosas que no existen. |
|
|
|
|
|
| Vamos al tercer gráfico, el más clásico. |
|
|
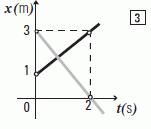 |
Siempre mirando el modelo:
x = xo + v ( t – to )
La gráfica negra:
x = 1 m + 1 m/s t
La gráfica gris:
x = 3 m – 1,5 m/s t
|
|
|
|
Y el encuentro:
1 m + 1 m/s tE = 3 m – 1,5 m/s tE
1 m/s tE + 1,5 m/s tE = 3 m – 1 m
2,5 m/s tE = 2 m
tE = 2 m / 2,5 m/s
|
|
|
| |
xE = 1,8 m; tE = 0,8 s |
[3] |
|
|
|
| Vamos con el 4to. que es medio raro. Lo voy a aprovechar para hacerlo más raro todavía. En lugar de elegir como iniciales los puntos (0;0) voy a elegir el otro. |
|
|
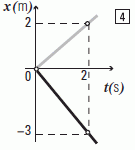 |
Siempre mirando el modelo:
x = xo + v ( t – to )
La gráfica negra:
x = –3 m – 1,5 m/s ( t – 2 s )
La gráfica gris:
x = 2 m + 1 m/s ( t – 2 s )
|
|
|
|
Si les pedimos que hablen del encuentro, en conjunto nos deben contestar (0;0).
xE = –3 m – 1,5 m/s ( tE – 2 s )
xE = 2 m + 1 m/s ( tE – 2 s )
Dos ecuaciones con dos incógnitas... esto es una papa. |
|
|
|
|
|
| Vamos al 5to gráfico. Decime vos qué elegí como "inicial" para cada móvil (le pongo comillas porque que sea o que no sea inicial es irrelevante para armar la ecuación). |
|
|
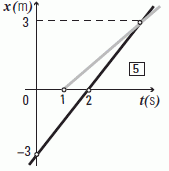 |
Siempre mirando el modelo:
x = xo + v ( t – to )
La gráfica negra:
x = –3 m + 1,5 m/s t
La gráfica gris:
x = vGris ( t – 1 s )
|
|
|
|
Oh... qué problema. Pero sigamos adelante. Sabemos que se encuentran en la posición xE = 3 m. Entonces, las ecuaciones dirán:
3 m = –3 m + 1,5 m/s tE
3 m = vGris ( tE – 1 s )
Nuevamente dos ecuaciones con dos incógnitas... otra papa (cocinala vos). |
|
|
| |
xE = 3 m; tE = 4 s, vGris= 1 m/s |
[5] |
|
|
|
| Vamos al último. La principal enseñanza de este caso es que tenés que aprender que lo más importante para leer un gráfico es mirar la magnitud de cada variabe. En este caso no se trata de posición sino de velocidad. |
|
|
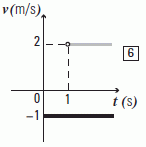 |
Ese gráfico no nos informa cuál es la posición ni la "inicial" ni ninguna otra, de modo que nos resulta imposible armar las ecuaciones. Lo más aproximado que podemos hacer sería ésto:
La gráfica negra:
x = x0N – 1 m/s t
La gráfica gris:
x = x0G + 2 m/s ( t – 1 s )
|
|
|
|
| Es casi seguro que en algún momento, en algún lugar, esos dos móviles se encuentren, pero no podemos averiguarlo. |
|
|
Desafío: Para el caso [6], hallar x0N y x0G para que el encuentro se produzca en xE = 2 m, tE = 2 s. |
|
 |
| |
|
| Algunos derechos reservados.
Se prohibe estrictamente leer este ejercicio resuelto por encima: hay que leerlo despacio y con atención. Las penalizaciones a esta infracción son severísimas. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| |

