 |
NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Funciones
|
|

|
| |
FIS a1.10- A partir del gráfico y = x², representar
gráficamente las siguientes funciones cuadráticas
indicando, en cada caso, si se produjo un
desplazamiento vertical, horizontal o cambio de
la concavidad.
a) y = — 2x²
b) y = (x — 5)²
c) x² + 4 — y = 0
|
| |
OK, nos están pidiendo que comparemos las tres parábolas representadas por esas tres ecuaciones con la parábola más sencilla y = x². Vamos de a una: |
|
|
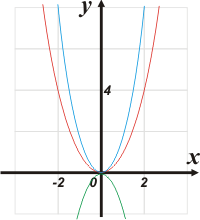 |
En rojo representé la parábola base: y = x².
En verde la del ejercicio: y = — 2x². Lo que ha cambiado es la concavidad, no sé si se nota que es más aguda, más afilada. Cuanto mayor sea el módulo del coeficiente cuadrático más aguda es la parábola. Y cuanto más se aproxima a 0, más ancha y gorda. Si el coeficiente valiese 0, tendríamos una recta, no una parábola.
También se ve que al ser negativo la concavidad se invierte y nos queda una parábola triste.
Tal vez no te des cuenta que es más angosta, por eso te representé, también, en celeste su simétrica: y = 2x², que es más fácil de comparar. |
|
|
|
| Vamos a la segunda. |
|
|
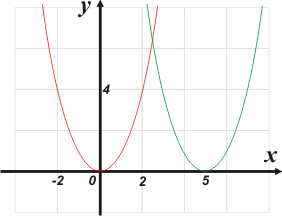 |
En rojo representé: y = x².
En verde, la que hay que comparar: y = (x — 5)². Fijate que es la misma parábola pero desplazada 5 unidades hacia la derecha. Es lógico, ya que el paréntesis nos está diciendo que nuestra variable está corrida en 5 unidades. Siempre que podamos ver la variable de esta manera, ya podés predecir cómo resultará la gráfica.
Pero no siempre es fácil de ver esto. La misma ecuación podría estar escrita de esta manera: |
|
|
|
y = x² — 10 x + 25, que es el modo tradicional. De modo que aunque teníamos un efecto interesante, no siempre vamos a poder verlo.
Vamos con la última, que es bien sencilla. |
|
|
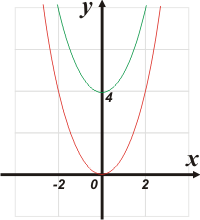 |
En rojo representé la parábola base: y = x².
En verde la del ejercicio: x² + 4 — y = 0. Que la voy a escribir así para que se te facilite la comparación: y = x² + 4. Ahí se ve claramente que la única diferncia con la original es el término independiente, 4, que es justamente la cantidad de unidades que la parábola se desplazó hacia arriba.
El término independiente es también la ordenada al origen. (El valor de y cuando x vale cero). |
|
|
|
| Si querés estudiar un poco más a fondo cómo inciden los coeficientes de una ecuación cuadrática en la geometría de la parábola que representan, podés entrar aquí y aquí, y divertirte un cacho. |
|
|
| |
|
|
| DESAFIO: ¿En qué punto se cortan las parábolas del segundo caso? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina. |
|
|
| | |
|
|

