home  | más de cinemática | otros temas de Física | lecciones del maestro Ciruela | tonterías |  @ 
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Movimiento uniformemente variado)
NMS c3.24 - ¿En qué se diferencian los gráficos posición-tiempo de los MRUV que poseen todas sus constantes iniciales iguales a excepción de la velocidad inicial?
  manolito

Te recomiendo enfáticamente este ejercicio. Su potencialidad para fijar conocimientos y establecer conexiones entre saberes que ya poseés y que relacionarlos entre sí los va a reforzar es enorme. También se lo recomiendo a mis colegas, que lo practiquen en sus cursos y si es posible en el aula, con un ida y vuelta permanente con los estudiantes.

Primero deberemos recordar que la gráfica posición tiempo de un MRUV debe representar la ecuación:

x = xo + vo ( t – to ) + ½ a . ( t – to )²

en la que las constantes iniciales (que ya sabés que no necesariamente se corresponden con el inicio del movimiento) son las que escribí en azul: to, xo, vo y a; y las variables son x y t (posición e instante).

En este ejercicio vamos a comparar varios gráficos de movimientos cuyas ecuaciones difieren exclusivamente en la velocidad inicial (que, entonces, se transforma en la variable del ejercicio):

x = xo + vo ( t – to ) + ½ a . ( t – to )²

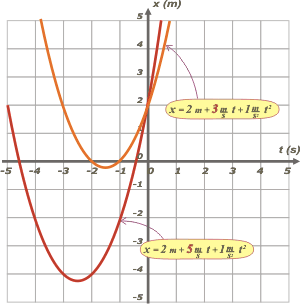
tomemos valores cualesquiera (los elegí a propósito sencillos para graficar sin dificultades) to= 0 s, xo = 2 m y a = 2 m/s². Entonces la ecuación básica (común a todos los movimientos que vamos a comparar) será:

x = 2 m + vo t + 1 m/s² . t²

Ahora le doy algunos valores arbitrarios a vo y grafico la parte interesante a ver qué nos va quedando.

    
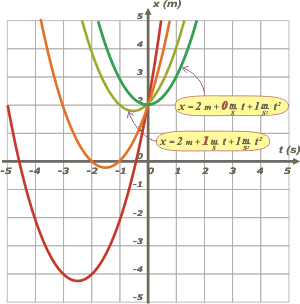
Cinemática - No me salen - Ricardo Cabrera

Lo vamos a hacer de a poco para que puedas ir observando las características de los movimientos representados, qué cosas tienen en común y qué cosas diferente.

Acá hay dos movimientos solos. En rojo:

   x = 2 m + 5 m/s t + 1 m/s² . t²

y en naranja:

   x = 2 m + 3 m/s t + 1 m/s² . t²

Lo primero que salta a la vista es que que ambas son parábolas, lo cual es obvio porque ambos son MRUV.
   

Lo segundo que también salta a la vista es que esas dos parábolas son idénticas. Es cierto: la forma de la parábola la da la aceleración. Y como ambos movimientos tienen la misma aceleración, las parábolas deben ser idénticas.

Lo tercero es que ambas pasan por la misma posición en el mismo instante, lo cual no podría ser de otro modo ya que para ambas: to= 0 s, xo = 2 m.

Por último: en ese punto las inclinaciones de las parábolas son diferentes: está más inclinada la roja que la naranja. Esa inclinación representa la velocidad en ese instante, y eso no es otra cosa que vo.

Te agrego dos curvas más:

    
Cinemática - No me salen - Ricardo Cabrera

La que está en verde clarito es:

   x = 2 m + 1 m/s t + 1 m/s² . t²

Y en verde oscuro:

   x = 2 m + 0 m/s t + 1 m/s² . t²

Esta última la podría haber escrito así:

   x = 2 m + 1 m/s² . t²

pero preferí consignar el valor de la velocidad inicial para que aprecies que lo que estoy haciendo es disminuir ese valor: 5, 3, 1, 0.
   

Podemos apreciar las mismas características de conjunto que resalté antes... pero ya aparece una nueva. Pareciera ser que variar la velocidad inicial equivale a desplazar la misma parábola en torno al punto to= 0 s, xo = 2 m. Como si ahí hubiese un clavo y solo puede desplazarse hacia la izquierda pasando por arriba.

Voy a agregar tres curvas más. Este gráfico viene con bonus track.

    
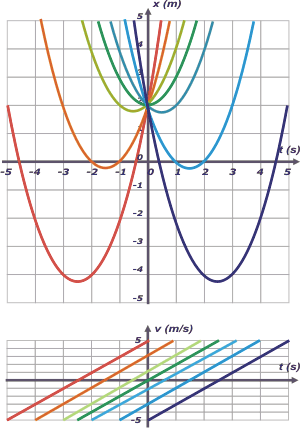
Cinemática - No me salen - Ricardo Cabrera

Las curvas agregadas son, en celeste:

   x = 2 m – 1 m/s t + 1 m/s² . t²

En turquesa:

   x = 2 m – 3 m/s t + 1 m/s² . t²

Y en azul:

   x = 2 m – 5 m/s t + 1 m/s² . t²

Con esto hacemos un recorrido bastante representativo de valores de velocidad inicial: 5, 3, 1, 0, -1, -3 y -5.

Fijate que las tres curvas agregadas tienen inclinación negativa en el instante to= 0 s.

El gráfico de velocidades se corresponde con el de posiciones, tienen la misma escala de tiempo y nos muestra cómo varía la velocidad de cada móvil representado.
  el vértice de cada parábola tiene una inclinación nula (és es la definición de vértice, aunque no la única), y coincide, lógicamente con una velocidad igual a cero

Prestá suma atención a la correspondencia entre ambos gráficos. Mirá cómo para cada movimiento (cada color) la velocidad se hace nula en cierto instante, qué valor tiene en to, cómo son las inclinaciones de todas las curvas (son paralelas, y no podría ser de otro modo, porque todos los movimientos representados tienen la misma aceleración), etcétera.

Si tenés ganas de practicar un poco de confección de gráficos acá tenés la tabla. Probá encontrarlos sin calculadora. Yo ya agregué algunos.

    
    ecuación ( vo) t (s) –5 –4 –3 –2 –1 0 1 2 3 4 5
                             
    x = 2 m + 5 m/s t + 1 m/s² . t² x (m) 2 –2 –4 –4 –2 2 8 16      
                             
    x = 2 m + 3 m/s t + 1 m/s² . t² x (m)           2          
                             
    x = 2 m + 1 m/s t + 1 m/s² . t² x (m)           2          
                             
    x = 2 m + 0 m/s t + 1 m/s² . t² x (m)           2          
                             
    x = 2 m – 1 m/s t + 1 m/s² . t² x (m)           2          
                             
    x = 2 m – 3 m/s t + 1 m/s² . t² x (m)           2          
                             
    x = 2 m – 5 m/s t + 1 m/s² . t² x (m)           2          
   
Si este ejercicio te pareció interesante, no dejes de hacer el siguiente.    
DESAFIO: Animate a agregar a mano alzada y cualitativamente el gráfico de este movimiento: x = 2 m – 1,5 m/s t + 1 m/s² t².   Ricardo Cabrera
Algunos derechos reservados. Se permite su reproducción citando la fuente. También está permitido imprimirlo, prestarlo, regalarlo, donarlo y algunas otras cosas más que terminan en arlo. Última actualización jul-12. Buenos Aires, Argentina.