| home | | | más sobre termo | | | otros temas de Física | | | lecciones del maestro Ciruela | | | tonterías | | | @ |
| NO ME SALEN (APUNTES TEÓRICOS DE BIOFÍSICA DEL CBC) EVOLUCIONES REVERSIBLES DE GASES IDEALES |
|
|||||||||||||||||||||||||||||||
ΔU, la variación de la energía interna en los gases ideales. Si llenás un globo con una mezcla de aire y gas de la hornalla de la cocina, y después le acercás un fosforito prendido (¡no lo hagas!, o si lo hacés, y sobrevivís, ¡no digas que sacaste la idea de acá!) vas a comprender que en ese gas, aparentemente inofensivo había encerrada una cantidad de energía insospechada. Efectivamente, algunos cuerpos pueden almacenar energía internamente de formas variadas, generalmente química. En cambio, los cuerpos simples, por ejemplo los gases ideales, la única forma de energía interna que poseen es el movimiento de agitación de sus moléculas, es la energía cinética de sus moléculas, y cuya manifestación grupal es la temperatura. De modo que para los gases ideales la energía interna, U, es una función -únicamente- de la temperatura absoluta del gas. Esto ayuda a comprender que: |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
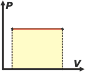
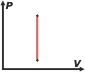
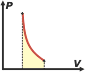
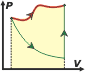
¿Qué significa que es una función de estado?. Significa que no depende de nada más que lo que se puede medir en el momento, no depende de la historia del sistema, no depende de un proceso. Por ejemplo, si querés conocer la temperatura de un cuerpo te basta con colocar un termómetro y hacer una lectura. Entonces podés inferir que la temperatura también en una función de estado, obtenés el dato en el momento y no se requiere información de otro tiempo. En cambio, si querés calcular el trabajo que realiza un gas entre dos momentos, entre dos instantes, entre dos estados o entre dos lo que sea, necesitás conocer la historia del proceso, la sucesión de estados intermedios por los que pasó. El trabajo, y el calor, por ejemplo, no son funciones de estado. Esto explica una particularidad interesante del cuadro de evoluciones típicas de los gases ideales que armé acá. Habrás notado que, curiosamente, en todas las evoluciones en las que termina habiendo un cambio de temperatura, el cálculo de la variación de energía interna, ΔU, se calcula de la misma manera:
Y -dicho sea de paso- cuando no hay cambio de temperatura esa relación sigue teniendo validez. La explicación la encontrás en los párrafos anteriores: la energía interna de un cuerpo simple depende solamente de su temperatura. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
Tal vez, genere un poco de ruido el hecho de que aún independientemente del tipo de evolución que realice un gas ideal, el cálculo de la variación de energía deba realizarse utilizando el calor específico molar a volumen constante, cv, cuando, por ejemplo, la evolución ocurrió a presión constante. Bien, te voy a demostrar (para la evolución isobárica) que el resultado es el correcto. Sólo necesito aplicar la ecuación de estado de los gases ideales, el primer principio de la termodinámica: Q = ΔU + W, y la relación (válida para todos los gases ideales independientemente del número de átomos de sus moléculas) cp – cv = R La evolución isobárica (evolución a presión constante) Admitamos que el trabajo que realiza el gas a presión constante se calcula de esta manera: p ΔV. Expresión que se deriva de la definición de trabajo mecánico para fuerzas constantes: W = F . Δx El calor intercambiado surge de la teoría de calorimetría por la cual, a menos que haya un cambio de estado de agregación de la materia, Q = m . c . ΔT, con las salvedades de que en este caso mediremos moles en lugar de masa, y usaremos calor específico molar a presión constante, cp, porque de ese modo evoluciona el gas, y de ese modo intercambia calor. Entonces Q = n . cp . ΔT. Luego, aplicando el primer principio, obtenemos:
Si describo los estados inicial y final con la ecuación de estado de los gases ideales:
A las presiones no les puse subíndice para distinguir el estado, ya que es la misma, no cambia durante la evolución. Ahora resto miembro a miembro las dos ecuaciones:
Saco factores comunes; en el primer miembro p y en el segundo n R
Si reemplazo esto en la expresión de la variación de energía interna tenemos:
Ahora saco como factor común n ΔT
Y por la relación que existe entre los calores molares a presión constante y volumen constante, reemplazamos y obtenemos:
¿Viste? Se trata de un resultado independiente de la transformación. Es una variación entre estados. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
| CHISMES IMPORTANTES | ||||||||||||||||||||||||||||||||
|
 |
|||||||||||||||||||||||||||||||
| PREGUNTAS CAPCIOSAS | ||||||||||||||||||||||||||||||||
|
 |
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||