ΔU, the variation of the internal energy in the ideal gases.

State function.

If you fill a balloon with a mixture of air and propane (the gas used by the stove), and then you strike a match near it (don't do it!, or if you do it and survive, don't say your idea came from here!) you 'll understand that in that apparently innocuous gas inside the balloon, there is enclosed an unsuspected amount of energy.

Indeed, some bodies can store energy internally in varied ways, usually in a chemical way. In contrast, when we talk about simple bodies, for example ideal gases, the only form of internal energy that they possess is the agitation movement of their molecules: the kinetic energy of their molecules, and whose group manifestation is the temperature.

So for ideal gases, the internal energy, U, is a function of the absolute temperature of the gas. This helps to understand that:

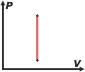
What does it mean that is a state function? It means that it depends on nothing else but what can be measured at the moment, it doesn't depend on the “history” of the system and it doesn't depend on a process. For example, if you want to know the temperature of a body, you just have to use a thermometer. Then, you can infer that the temperature is also a state function, obtained only using the information of an instant in time, and without requiring any other data.
On the other hand, if you want to calculate the work done by a gas between two instants, between two states or between two whatever, you need to know the "history" of the process, the succession of intermediate states through which it happened. Work, and heat, for example, are not state functions.
This explains an interesting property of the table of ideal gases' typical evolutions, that I showed here. You will notice that, curiously, in all the evolutions in which occurs a change of temperature, the calculation of the internal energy variation, ΔU, is calculated in the same way:

ΔU = c_v n ΔT

And - by the way - when there is no change in temperature, that relationship is still valid. The explanation is found in the previous paragraphs: the internal energy of a simple body depends only on its temperature.

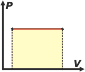
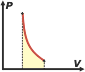
Perhaps it might sound strange the fact that even regardless of the type of evolution an ideal gas has, the calculation of the energy variation should be made using the specific molar heat at constant volume, cv, when, for example, Evolution occurred at constant pressure. Well, I'll show you (for isobaric evolution, as an example) that the result is correct.

I only need to apply the equation of state of ideal gases, the First Law of Thermodinamics: Q = ΔU + W, and the relation (valid for all ideal gases regardless of the number of atoms in their molecules) c_p – c_v = R

Isobaric evolution (evolution at constant pressure)

We assume that the work performed by the gas at constant pressure is calculated as:
p ΔV, expression deducted from the definition of mechanical work for constant forces:
W = F. Δx

The expression fot the heat exchanged arises from the theory of calorimetry. Because of it, unless there is a change in the aggregation state of  matter; Q = m. C. ΔT, but we have to take in consideration  that in this case we will measure moles instead of mass, and we will use specific molar heat at constant pressure, c_p, because that's the way in which gas evolves, and in that way it exchanges heat.

Applying the First Law, we can know that:

ΔU = Q – W

ΔU = n c_p ΔT – p ΔV

If I describe the initial and final state with the equation of state of the ideal gases:

p V_F = n R T_F

p V₀ = n R T₀

I didn't use subindex with pressures to distinguish the state since it is the same and doesn't change during evolution. Now  I subtract "term by term" both equations:

p V_F – p V₀ = n R T_F – n R T₀

Now we can express it using differentials:

p ΔV = n R ΔT

If I replace that in the expression of the internal energy variation, we have that:

ΔU = n c_p ΔT – n R ΔT

Now I take as a common factor n ΔT

ΔU = ( c_p – R ) . n ΔT

And because of the relationship between the molar heats at constant pressure and constant volume, we replace and obtain:

ΔU = c_v n ΔT

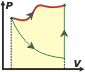
See? It is a result which is independent from the transformation. It is a variation between states.

CURIOUS FACTS

CAPTIOUS QUESTIONS

• Why is the equation of state of ideal gases, P V = n R T, called “equation of state”?
  • What is the definition of ideal gas?