 |
NO ME SALEN
(APUNTES TEÓRICOS DE BIOFÍSICA DEL CBC)
TRANSFORMACIONES REVERSIBLES E IRREVERSIBLES
|
|

|
| |
REVERSIBLES, IDEALES, DEFINIDAS
Es muy importante entender eso de las transformaciones reversibles, entre otras cosas, porque la definición de entropía requiere de la idea de calor intercambiado en una reacción reversible, Qrev. |
| |
| |
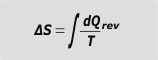 |
variación de entropía |
|
|
|
Las transformaciones reversibles no existen. En nuestro universo está prohibido volver atrás. Una pequeña porción de universo sí puede volver atrás (por ejemplo: nada te impide volver a leer este apunte desde el principio porque te diste cuenta que requiere ser leído con más atención)... pero el universo, en su conjunto, no puede.
Y si las transformaciones reversibles no existen... ¿a qué nos referimos cuando hablamos de ellas? Nos estamos refiriendo justo a ese límite infranqueable, al que nos acercamos tanto como querramos (mentalmente), o podamos (físicamente), pero que nunca podremos alcanzar. Es lo que se llama una transformación ideal.
¿Qué características tienen esas transformaciones ideales, reversibles?
- la variación de entropía total (la del sistema que consideres más la del medio en que ocurre) es nula
- todos los pasos intermedios están definidos (se conocen con certeza)
- ocurren muy lentamente
- pueden ser las más eficientes
- no existen en nuestro universo, pero marcan un límite que es útil conocer
De todas las características la única definitiva (por sí solo alcanza para definirla) es la primera, o sea, que la variación de entropía total sea nula.
Una máquina térmica reversible (ideal, de Carnot)
El primero en imaginar una máquina térmica que funcione de manera reversible fue el físico y militar francés Sadi Carnot en 1822. Y concluyó que tal máquina tendría el máximo rendimiento posible. Aunque llegó a esa conclusión acertada partiendo de premisas erróneas (pensaba que el calor era un fluido invisible y perenne) a partir de entonces a las máquinas "reversibles" también se las llama "de Carnot". |
|
|
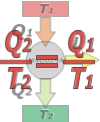 |
La máquina de Carnot no viola el 2do. Ppio. De modo que la entropía total en el del proceso aumente, ΔSU > 0. Pero como el segundo principio no dice cuánto debe aumentar, diez veces, un décimo, un centésimo, un millonésimo... podemos llevar la situación al límite y decir que en esa situación ideal se estará cumpliendo que:
ΔSU = 0
Es una situación límite, no te olvides... será un artificio matemático, pero es muy útil para tenerlo en cuenta desde la física. |
|
|
|
Que ΔSU = 0 significa que:
ΔSmedio + ΔSmáq + ΔScaldera = 0
donde el medio es la fuente 2, la caldera es la fuente 1, y máq es la máquina térmica propiamente dicha. Tanto la caldera como el medio funcionan a temperatura constante (por eso se las llama fuente), lo que nos permite expresar la suma de entropías así:
(Q2/T2) + ΔSmáq – (Q1/T1) = 0
La variación de entropía de la máquina vale cero (ΔSmáq = 0), porque actúa cíclicamente, regresando constantemente a su estado inicial (y como la entropía es una función de estado no puede variar). Y a la variación de entropía de la fuente 1 (la caldera) le puse signo negativo porque cede calor (en cambio el medio lo recibe). Nos queda esto:
(Q2/T2) – (Q1/T1) = 0
que podemos escribir así:
(Q2/T2) = (Q1/T1)
Y de donde surge esta relación tan interesante:
(Q2/Q1) = (T2/T1)
Acordate que esta igualdad sólo se establece en máquinas ideales.
El rendimiento de esta máquina ideal (máximo rendimiento posible de una máquina térmica) será:
η = 1 – (Q2/Q1) = 1 – (T2/T1)
Carnot se ocupó también de describir cómo podría funcionar una máquina de estas características, e ideó una que evolucionara cíclicamente entre dos isotermas y dos adiabáticas. Ese tipo de ciclos llevan hoy por nombre "ciclos de Carnot".
¿Qué significa que no aumente la entropía?
Un ingeniero mecánico está interesado en la reversibilidad y en las variaciones de entropía porque ha visto que cuando las máquinas funcionan se pierde energía, o sea, se pierde guita. Pero el aumento de entropía en realidad describe el exceso de energía que se pierde. Si la entropía está aumentando lo que el ingeniero está perdiendo es la oportunidad de usar parte de esa energía térmica para transformarla en trabajo mecánico. |
|
|
 |
Es imposible extraer calor de una única fuente y hacer funcionar una máquina cíclica, eso ya lo sabe; la máquina funciona entre dos fuentes, una caliente y otra fria, extrayendo calor de una y entregándosela a la otra, y disponiendo de una buena oportunidad de tomar parte de ese calor para producir trabajo mecánico... hasta ahí todo Ok.
Una vez que las fuentes han alcanzado la misma temperatura, esta oprtunidad está irremediablemente perdida. |
|
|
|
Por lo tanto cualquier proceso irreversible en una máquina térmica disminuye su rendimiento, es decir, reduce la cantidad de trabajo mecánico que puede obtenerse de una cierta cantidad de calor, absorbido de la fuente costosa. |
|
|
CHISMES IMPORTANTES |
|
|
- Carnot imaginaba una substancia -llamada "calórico"- que fluía desde una temperatura mayor hasta una temperatura menor. Igual que el agua, otro fluido, que cuanta mayor sea la diferencia de altura desde la que caía con más fuerza puede mover una noria, así, el calórico puede obtener más trabajo mecánico (o sea, más podía "mover" la máquina térmica) cuanta mayor sea la diferencia de temperaturas desde las que fluía. Errado, pero correcto.
|
|
 |
| PREGUNTAS CAPCIOSAS |
|
- ¿Por qué las centrales térmicas (las grandes usinas que convieten energía química de diversos combustibles en energía eléctrica) se hallan siempre a orillas de un río o en la costa marítima?
|
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco el aforismo de Ernesto Esteban Etchenique, "Cuando alcancé la Sabiduría, ella me miró y dijo: ‘Ya me alcanza cualquiera’". Última actualización jul-09. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|

