NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
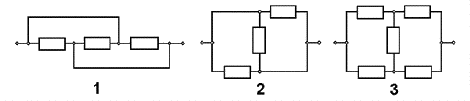
EM 8) Los resistores de las figuras tienen todos una resistencia de tres ohms. ¿Cuánto vale la
resistencia equivalente en cada caso?
a) 1Ω, 1Ω, 1Ω b) 1Ω, 3Ω, 3Ω c) 3Ω, 1Ω, 3Ω
d) 1Ω, 1Ω, 3Ω e) 3Ω, 3Ω, 3Ω f) 3Ω, 1Ω, 3Ω |
|
|
| |
Hay quien lo mira a un metro y en 10 segundos lo saca. Hay quien lo estudia con lupa 18 horas seguidas y justo antes de desmayar de sueño decide pasarse a abogacía. Pero fijate que si tenés un método (y hay más de uno) el asunto sale con fritas.
El método que te ofrezco consiste en usar colores para pintar los cables. En un circuito los cables son las líneas llenas que unen resistencias o capacitores o pilas o lo que sea. La cuestión es que los cables son conductores ideales (sin resistencia) y por lo tanto tienen el mismo potencial en toda su extensión. Y si en algún lugar hacés un nudo y empalmás otro cable, ese otro cable que sale del nudo también tiene el mismo potencial.
Entonces elegís un color cualquiera y comenzás a pintar todo el cable que puedas sin pasar por arriba de ningún componente (en este ejercicio: ninguna resistencia). Si te quedó cable sin pintar seguís con otro color. Y así por todo el circuito.
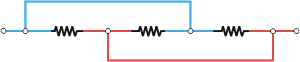
Mirá: acá va para el circuito 1. |
|
|
 |
|
|
Y ahora mirás una por una cada resistencia y te fijás a qué potenciales está conectada. En este caso las tres resistencias están conectadas de la misma manera: cada extremo a un potencial diferente entre los únicos dos que hay. De modo que las tres resistencias están agrupadas en paralelo.
Como intuyo que no me creés, voy a deformar el circuito, en dos pasos, para llegar al paralelo de las tres resistencias tan difícil de ver en el original. |
|
|
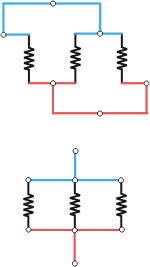 |
Hacé de cuenta que los cables son más o menos elásticos. Tirá del azul hacia arriba y del rojo hacia abajo. Las resistencias se van a rotar, ¿no es cierto?
Las resistencias no tienen polaridad, no cambia su valor si las conectás al derecho o al revés; no tienen derecho ni revés.
Los nudos de los cables se pueden correr, los cables se pueden alargar o acortar... la única condición es que se mantengan las conexiones originales con los componentes del circuito. Si necesitás más pasos intermedios hacelos vos, te viene bien como práctica, ya que la "deformación de los circuitos" es otro método -y bastante utilizado- para simplificar y comprender circuitos.
En este caso se llega a lo que ya habíamos deducido: las tres resistencias están en paralelo. |
|
|
|
La resistencia equivalente a un grupo de tres resistencias en paralelo, de 3 Ω cada una, vale 1 Ω.
Vamos al segundo circuito. Mirá qué fácil es entenderlo y resolverlo utilizando la técnica de los colores: |
|
|
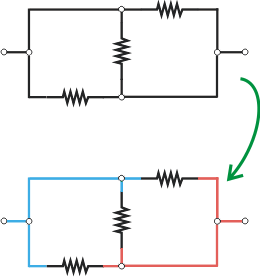 |
Tomás el circuito original, agarrás las pinturitas y arrancás con un color desde un estremo del circuito. Seguís con el mismo color hasta llegar a una resistencia (también podría ser un capacitor o cualquier otro elemento eléctrico).
Pero los nodos no cambian los colores. Todos los cables que llegan o salen de un nodo (los redondelitos blancos) tienen el mismo color.
Del otro lado de la resistencia usás otro color. Terminás cuando todo el circuito está coloreado. Y lo mirás de lejos.
Quedó clarísimo, en este caso, que se trata de un simple y sencillísimo paralelo entre tres resistencias (que encima son iguales entre sí). |
|
|
|
Te dejo a vos las cuentas (tenés que hacerlas mentalmente), y encontrarás que la resistencia equivalente de este circuito es la misma que el anterior: 1 Ω.
El tercer circuito es un caso especial. Te conviene primero estudiar este ejercicio.
Resulta que tiene un complejidad que nos excede... y una solución inesperada. Pasa que las asociaciones serie y paralelo no son las únicas posibles (aunque sí las más corrientes y útiles). Pero hay configuraciones, como la del ejercicio 3 que no se encuadra en los casos conocidos. Para resolver esas configuraciones (que reciben el nombre de estrellas o mallas) los físicos y técnicos disponen de otras herramientas analíticas: las leyes de Kirchoff. Aunque se trata de una serie de ecuaciones sencillas, el método de resolución de circuitos con las leyes de Kirchoff suele quedar fuera de los cursos iniciales de Física y no vale la pena que nos metamos en él. |
|
|
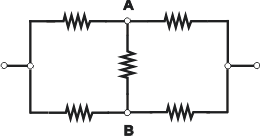 |
La configuración 3 es típica para la aplicación del método de Kirchoff porque es sencilla valgan lo que valgan cada una de las cinco resistencias que la integran.
Pero en el caso concreto de nuestro circuito 3 no hace falta Kirchoff, y lo podemos resolver nosotros con lo que ya sabemos de Ley de Ohm, porque al ser que todas las resistencias valen lo mismo (3 ohms cada una) la diferencia de potencial entre los punto A y B vale cero. |
|
|
|
De modo que la resistencia del centro -al no estar sometida a una diferencia de potencial distinta de cero- no es atravesada por ninguna corriente, es lo mismo que esté a que no esté. Podés ignorarla. Y lo que queda es un simple paralelo integrado por una simple serie en cada rama. Y la resistencia equivalente de todo el circuito (hacemos las cuentas mentalmente) vale 3 Ω.
Y así llegamos a la respuesta final de este ejercicio kilométrico (por no decir kilombétrico).
|
|
 |
| |
| |
| |
|
|
| Desafío: Aplicá el método de los colores al tercer circuito, a ver qué pasa. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

