NO ME SALEN
(APUNTES TEORICOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
ELECTROSTATICA - CAMPO ELECTRICO
|
|

|
| |
CAMPO ELECTRICO
La idea de campo se basa en transferirle las propiedades eléctricas al espacio. De modo que si colocamos una carga cualquiera en una posición cualquiera y observamos que una fuerza eléctrica actúa sobre ella, no es necesario inferir ni buscar qué carga, o cuáles cargas, están interactuando con ella: decimos, simplemente, "le ocurre lo que le ocurre por estar en un campo eléctrico".
Es una idea fecunda que excede la cuestión eléctrica, y permite esquivar el espinoso asunto de las fuerzas que actúan a distancia, algo que nunca terminó de cerrarle del todo a todos.
|
| |
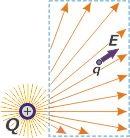
Te voy a hacer el razonamiento a mi manera. Ponele que en algún lugar hay una carga lo suficientemente grande como para influir en un espacio generoso alrededor suyo. Esa carga la voy a designar con una Q mayúscula, y solemos llamarla carga fuente.
A mí sólo me interesa la región de mi laboratorio -el rectángulo punteado en azul- de modo que no pienso salirme de él... y lo voy a recorrer íntegramente acompañado de una pequeña carga de prueba, q minúscula, que solemos llamar carga exploradora.
Tomo nota del módulo, dirección y sentido de la fuerza que recibe mi carga exploradora, Fe... y defino campo eléctrico, E, de esta manera: |
 |
|
|
|
|
|
|
Así definido, el campo eléctrico es una entidad independiente de la carga con la que exploro el lugar que se describe, e independiente también de la fuerza que ésta reciba; aunque no lo parece, su definición así lo indica. Veamos: |
|
|
| E = |
|
Fe |
= |
ko Q q |
la carga exploradora se cancela |
|
|
| q |
q d² |
|
|
|
| Como ves, sólo depende de la carga generadora del campo (Q, la carga fuente) y de la distancia entre ella y el punto en el que se describe el campo. |
|
|
|
|
|
La expresión de arriba permite conocer el valor del campo generado por una carga puntual.
Pero cualquier lugar del espacio puede estar afectado por las contribuciones de campo generado por varias (o muchas) cargas. Para conocer el valor y las características del campo en esos lugares hay que sumar las contribuciones individuales que hace cada carga puntual. El campo en un punto cualquiera será igual a la suma vectorial de las contribuciones de campo generado por cada una de las cargas de la vecindad.
De cualquier forma el campo se define de la misma manera, o sea, para un punto del espacio y como el cociente entre la fuerza eléctica que recibiría una carga de prueba y el valor de la carga (E = Fe / q), y siempre va a ser una propiedad del espacio, y no de la carga que metas en él para ver cómo reacciona.
Las unidades en las que deberemos medir los campos eléctricos serán: |
|
|
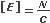
|
|
|
| (la unidad de campo es: newton sobre coulomb). Este cociente entre unidades tiene varios equivalentes que no falta mucho para que entiendas, pero igual te adelanto uno: |
|
|
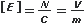
|
|
|
(el campo también puede medirse en volt sobre metro, pero no te intranquilices... esa parte ya llega).
Líneas de campo
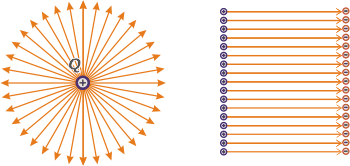
El campo es una magnitud vectorial, o sea: no sólo hay que decir cuánto vale... también hay que decir hacia dónde apunta. En el esquemita que te hice arriba figuran una líneas muy interesantes porque describen la configuración geométrica del campo. Reciben el nombre de líneas de campo (tienen propiedades muy estrictas con las que no te voy a abrumar) y en los libros de física podés encontrar las configuraciones (o espectros) de los campos más famosos. Acá te voy a mostrar sólo dos, que son aquellos que mayor importancia biológica tienen: el campo producido por una carga puntual, y el campo uniforme. |
|
|
 |
|
|
El campo uniforme se produce cuando se tienen dos planos paralelos cargados uniformemente con cargas opuestas. Es exactamente lo que ocurre en la membrana plasmática de todas las células (¿te acordás de la bicapa lipídica?) y en su pariente de la rama de los ingenieros: el capacitor de placas paralelas.
En esa región del espacio, tan interesante desde muchos puntos de vista, el campo eléctrico uniforme se calcula de la siguiente manera: |
|
|
|
|
|
donde σ (sigma) es la densidad de carga, o sea el cociente entre la carga total que hay en uno de los planos, y el área del plano ( σ = Q / A ); y εo es la permitividad del vacío, un pariente cercano de ko, la constante de Coulomb... o sea, una constante de proporcionalidad.
εo = (12,57 ko)-1
|
|
|
| εo = 8,85 x 10-12 |
|
C² |
|
|
| N m² |
|
|
|
Fijate que las unidades resulten las de campo (y me quedo más tranquilo).
Cuando el campo eléctrico -por ejemplo el uniforme- se halla en un espacio material (no vacío) entonces la constante no será εo sino εo . εr. O sea, simplemente, se multiplica por el épsilon relativo (la constante dieléctrica) del material.
|
|
|
| |
|
| |
 |
|
|
CHISMES IMPORTANTES:
- La acumulación de cargas a uno y otro lado de la membrana celular (negativas en el interior, positivas en el exterior) resulta del trabajo realizado por las bombas de sodio-potasio, que para hacerlo consumen energía química en forma de ATP.
|
|
| PREGUNTAS CAPCIOSAS: |
|
- ¿Cuánto vale la densidad de carga en una membrana plasmática típica de un axón, si su espesor vale 5 nm y el campo eléctrico 108 N/C?
|
|
| |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-07. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|

