NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
 |
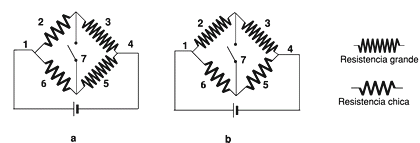
34) Sabiendo que R > r, ordene de mayor a menor las intensidades de corriente que circula
por los cables 1, 2, 3, 4, 5, 6 y 7 en el circuito a antes de cerrar el interruptor y después de
cerrarlo. Idem para el circuito b. |
| |
 |
|
| |
Este ejercicio tiene una trampa maléfica. (En realidad benéfica, porque te lo proponen en una ejercitación y no en un examen). Se trata de lo siguiente: los circuitos de este estilo, en los que la corriente puede tomar caminos alternativos que no se corresponden con la asociación serie/paralelo, y que los electrónicos llaman circuitos de mallas se resuelven gracias a las Leyes de Kirchoff, que -aunque son sencillas- suelen quedar afuera de los cursos secundarios y preuniversitarios. De modo que así, a primera vista, cualquier docente de Física diagnosticaría: este ejercicio corresponde a otro nivel.
Pero ocurre que éstos dos, en particular, poseen una propiedad inusual que permite resolverlos sencillamente con la Ley de Ohm, de modo que sólo hay que estar muy despierto para darse cuenta de esa circunstancia inusual.
Te voy a resolver el caso b que es más fácil de explicar. Empecemos con el interruptor abierto, de modo que sea imposible el paso de la corriente por ese conductor (de modo que la corriente 7 vale 0), ni lo dibujo. |
|
|
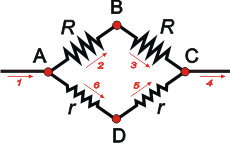 |
La corriente entrante (1) se divide en dos: 2 y 6. Como en la bifurcación no se muere ni nace ninguna carga es obvio que la suma de las corrientes 2 y 6 será igual a la corriente 1 (i2 + i6 = i1). Lo que también indica que la corriente 1 ha de ser mayor que cualquiera de las dos.
Por otro lado resulta obvio que las resistencias de la rama superior (ABC) están en serie. De modo que toda la corriente que pasa por la primera resistencia de la serie debe pasar por la segunda. Dicho de otro modo la corriente 2 es igual a la corriente 3 ( i2 = i3).
En la rama inferior (ADC) pasa lo mismo que en la de arriba, de modo que la corriente 6 es igual a la 5 (i6 = i5). |
|
|
|
Por último, si comparamos la rama superior con la inferior, vemos que la resistencia total de la serie superior (R + R), es mayor que la inferior (r + r). La diferencia de potencial (ΔVAC) es la misma para ambas series, ya que están en paralelo entre sí.
Y según la Ley de Ohm, a mayor resistencia menor corriente, de modo que la corriente que atraviesa la rama superior -de mayor resistencia- ha de ser menor que la corriente que atraviesa la rama inferior -de menor resistencia- (i2 < i6).
Si juntamos en una sola expresión todo lo que fuimos razonando, llegamos a: |
|
|
i1 = i4 > i5 = i6 > i2 = i3 > i7 = 0
|
|
|
|
Inventemos un ejemplo: la corriente 1 podría valer 10 A, se divide en dos, por arriba van 3 A y por abajo 7 A. Las corrientes vuelven a reunirse en C, de modo que la corriente 4 vuelve a valer 10 A. Fácil, ¿no?
Ahora vamos a resolver el mismo circuito, pero con la llave cerrada. Es acá donde hay que avivarse de la peculiaridad de este circuito.
Olvidate de la rama de abajo y prestale atención exclusivamente a la de arriba.
|
|
|
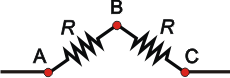 |
Las dos resistencias de esa rama son iguales entre sí, de modo que las caídas de tensión en cada una también serán iguales entre sí y, además, serán iguales a la mitad de la caída de tensión de la fuente. En símbolos:
ΔVAB = ΔVBC = ½ ΔVAC
Pongamos un ejemplo numérico: si la fuente proveyera una diferencia de potencial de 12V entonces podría ser:
VA = 12V, VB = 6V y Vc = 0V
|
|
|
|
Si realizás el mismo razonamiento para la rama de abajo, y le ponemos el mismo ejemplo numérico llegarás a la conclusión de que el potencial de D es el mismo que el de B. O sea: ΔVBD = 0V.
Para terminar, si unís con un cable (tenga mucha o poca resistencia) los puntos B y D, como entre ellos no hay diferencia de potencial, no habrá corriente alguna. O sea, que la llave esté abierta o cerrada (para esta particular configuración de resistencias) es lo mismo, por ahí no pasa corriente. La corriente 7 seguirá valiendo cero y el resultado es el mismo que el anterior.
El caso a es apenas más difícil que el anterior y se llega a la misma conclusión respecto de la corriente 7. Vos podés. |
|
|
| |
|
 |
| Desafío: Justificar con la Ley de Ohm todas las conclusiones intermedias que yo relaté verbalmente para no hacerte la vida imposible con ecuaciones, y porque me parecía que era más didáctico resolverlo verbalmente que con ecuaciones e inecuaciones. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción bajo la solemne promesa de citar la fuente con mucho amor y ternura. Última actualización jul-11. Buenos Aires, Argentina. |
|
|
| | |
|
|

