NO ME SALEN
(APUNTES TEORICOS Y EJERCICIOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
|
|

|
| |
Nee 01)* El esquema muestra dos cargas eléctricas fijas en los puntos A y E. El espacio entre ellas está dividido en cuatro partes de igual longitud. ¿Dónde habría que poner una tercera carga para que estuviera en equilibrio bajo la acción de las otras dos?
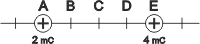
a) entre A y B b) entre B y C c) entre C y D
d) entre D y E e) a la izquierda de A f) a la derecha de E
|
|
| |
Este ejercicio está diseñado para que lo resuelvas por tanteo, colocando la tercera carga en distintos punto y luego viendo para dónde habría que correrla para que la fuerza que recibe de cada una sea igual. Lo vas a entender al toque, mirá:
No importa el signo ni la intensidad de la tercera carga, el resultado es el mismo e independiente de esto. Pensemos la cuestión cualitativamente como para calentar las neuronas; después hacemos el planteo formal.
Supongamos que la tercera carga, Q, la que agregamos, se trata de una carga positiva. Si la colocamos a la izquierda de A sería rechazada por ambas cargas fijas que la empujarían -ambas- hacia el mismo lado, hacia la izquierda: por ese lado no puede encontrar nunca el equilibrio. Vayamos del otro lado: a la derecha de E; le ocurriría lo mismo: no podría hallar el equilibrio. No le cabe otra alternativa que quedar intercalada entre las cargas fijas. En ese barrio va a estar rechazada por la fija en A hacia la derecha, y rechazada también por la fija en E hacia la izquierda. Si el rechazo con cada carga tiene la misma intensidad puede encontrar el equilibrio (inestable -por cierto- pero equilibrio al fin).
Coloquemos la tercera carga, Q, en el punto C a ver qué pasa. |
|
|
 |
|
|
| La fuerza con que la repele la carga que se halla en E, FE , es mayor (el doble mayor) que la repulsión con la carga que se halla en A, FA. Eso es fácil entender con sólo mirar la ley de Coulomb que describe ambas fuerzas: |
|
|
| |
|
k . Q . 2 mC |
< |
k . Q . 4 mC |
|
|
|
| dAC² |
dCE² |
|
|
|
Si cancelás los factores comunes o iguales podés chequear fácilmente la desigualdad.
Para que las fuerzas sean iguales habría que correr la tercera carga acercándola a la carga que está en el punto A. Así FA crecería (a menor distancia mayor fuerza) y la fuerza que hace la carga colocada en E disminuiría (a mayor distancia menor fuerza). Probemos entonces colocar la tercera carga en el punto B. |
|
|
 |
|
|
| Ahora la fuerza con que repele la carga situada en A es mucho mayor que la fuerza con que repele la otra. Mirá las fórmulas. |
|
|
| |
|
k . Q . 2 mC |
> |
k . Q . 4 mC |
|
|
|
| 1² |
3² |
|
|
|
Donde 1 y 3 son las distancias entre las cargas expresadas en unidades de distancia del gráfico adjunto al enunciado. (No sé cuánto valen esas unidades, pero no importa, las unidades son iguales entre sí).
Cancelando todos los factores comunes la desigualdad se hace más patente. Mirá: |
|
|
|
|
|
Si queremos que las fuerzas sean iguales habrá que correr la tercera carga hacia la derecha, así disminuye la fuerza que le hace la carga de 2 mC y aumenta la otra.
Y si lo pensás un poco, ya resolvimos el ejercicio, porque cuando la colocamos en C había que moverla hacia la izquierda, y cuando la colocamos en B hay que moverla hacia la derecha. Luego, la posición en la que las fuerzas se igualan debe estar entre B y C. |
|
|
| |
b) entre B y C |
|
|
|
El ejercicio también se puede plantear como para resolverlo con exactitud (tenés planteado casi exactamente el mismo problema en la guía de ejercicios de gravitación, acá).
Tomemos un sistema de referencia de posiciones con el 0 en A y sentido de aumento hacia B. Y supongamos que la distancia entre A y E vale 4 (las mismas unidades que usamos antes).
FA = FE
Luego, según la Ley de Coulomb: |
|
|
| |
|
k . Q . 2 mC |
= |
k . Q . 4 mC |
|
|
|
| x² |
(4 — x)² |
|
|
|
| Donde x es la distancia de la tercera carga con la de la izquierda y 4 — x es la distancia que la separa de la carga de la derecha. |
|
|
|
|
|
(4 — x)² = 2 x²
Sacamos raíz cuadrada en ambos miembros.
4 — x = 1,41 x
4 = 1,41 x + x
4 = 2,41 x
Con lo que obtenemos...
x = 1,66
|
|
|
|
b) entre B y C |
|
|
|
|
|
|
Desafío: ¿Por qué dije que el equilibrio es inestable? |
|
 |
| |
| |
| * Ejercicio tomado en el 2do. examen parcial de Ciudad Universitaria, en diciembre de 2007, en el Curso de Biofísica. |
|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Natalia Leto por el envío de una errata. Última actualización dic-07. Buenos Aires, Argentina. |
|
|
| | |
|
|

