 |
NO ME SALEN
(APUNTES TEORICOS DE BIOFÍSICA DEL CBC)
ELECTRICIDAD
ELECTROSTATICA - CAPACITORES
|
|

|
| |
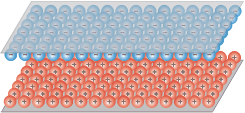
Poder juntar cargas del mismo signo en un espacio reducido es importantísimo, útil, práctico, rentable, divertido... pero harto difícil. Pasa que las fuerzas de repulsión entre las cargas la convierte en una tarea casi imposible: terminan expulsándose entre ellas debido a la acumulación de fuerza repulsiva, y salen volando para cualquier lado. Se intentó de muchas maneras y con varios materiales, pero terminan disparándose en un efecto que se dio en llamar viento eléctrico. Son rebeldes: no quieren juntarse.
Pero debido a un accidente que tuvo el lechero que abastecía a la Universidad de Leiden -en los Países Bajos- en 1746, se descubrió un método para armar un dispositivo súper sencillo e ingenioso que inicialmente recibió el nombre de condensador, ahora conocido como capacitor, y que es el tema de esta lección. |
| |
Consiste simplemente en disponer de dos placas metálicas paralelas, aisladas entre sí y lo más cercanas posible una de otra. Y por cada carga del mismo signo que se coloca en una de ellas, debe colocarse una del signo opuesto en la otra placa.
De esta manera uno puede alojar muchísimas cargas de un mismo signo en cada una de las placas ya que, si bien se van a estar repeliendo intensamente entre ellas, al mismo tiempo van a estar siendo atraídas fuertemente por las de la placa de enfrente. |
 |
|
|
|
Como las cargas habitan los materiales conductores no en su interior sino en la superficie, se van a colocar en las superficies interiores de las placas, enfrentadas a las cargas atractivas de la cara de enfrente.
De modo que es gracias a esa fuerza atractiva entre los grupos enfrentados que se logra equilibrar la fuerza repulsiva que hay dentro de cada grupo. Este tenso equilibrio es el secreto de los capacitores.
Un capacitor tendrá más capacidad (valga la redundancia) de albergar cargas cuanto más cercanas estén las placas (o sea: es inversamente proporcional a la distancia entre ellas) y -lógicamente- cuanto más grande sea el área de ellas (o sea: será directamente proporcional al área). La capacidad (o capacitancia), que se simboliza con la C, es la magnitud eléctrica característica de los capacitores, y está determinada, en principio, por esos dos parámetros: su área, A, y su distancia entre placas, d. (Más abajo añadimos un tercer parámetro). |
|
| Te garantizo que no se trata de un complot contra vos... pero es cierto: puede confundirte que el símbolo para la magnitud capacidad, C, sea el mismo que para la unidad de carga, coulomb, C... no tenés más remedio que juntar los mayores con los pulgares y decir: "ohm..." |
|
| |
|
|
donde εo es la permitividad del vacío, que funciona aquí como constante de proporcionalidad. Si recordamos que su valor es:
|
|
| |
resulta que las unidades en las que habrá que medir las capacidades (no surge del primer paso... tenés que hacer dos o tres reemplazos de unidades eléctricas) serán:
|
|
| 1 faraday = |
|
1 coulomb |
|
|
| 1 volt |
|
|
Esta relación entre unidades nos anticipa cuál es el comportamiento eléctrico de los capacitores; o sea, cuál es la relación entre las magnitudes eléctricas que intervienen en la acumulación de cargas. En efecto: la carga y la capacidad son directamente proporcionales ya que si aumenta la capacidad es porque hay más lugar para meter cargas. Por otro lado cuanto mayor sea la carga mayor será la tensión o diferencia de potencial entre ellas, ya que mayores serán las fuerzas de repulsión y atracción... por más que estén equilibradas.
Estas dos relaciones básicas se pueden juntar en una única expresión que describe el comportamiento eléctrico de los capacitores: |
|
| La carga neta de los capacitores siempre es cero (ya que siempre tiene tantas cargas positivas de un lado como negativas del otro). Pero lo que a nosotros nos interesa es la carga en cada una de sus placas: a eso lo llamamos Q. |
|
|
| capacidad = |
|
carga |
|
|
| voltaje |
|
|
|
| |
Si en el espacio entre las placas colocamos un material cualquiera (que sea aislante, porsupu), la capacidad del dispositivo se modifica. Para corregir el cálculo basta con incluir la constante dieléctica relativa del material, εr, junto a εo.
|
|
|
| |
|
|
Ese material aislante que se introduce entre las placas suele denominarse dieléctrico. La introducción del dieléctrico aumenta la capacidad del capacitor. Lejos de entorpecer la "comunicación" entre las cargas de las placas opuestas, produce un efecto de "acercamiento virtual" que permite albergar más carga (o bien, disminuir la tensión). Además ese intercalamiento de dieléctrico facilita la construcción del capacitor, de modo que casi todos los capacitores de placas paralelas los tienen.
El aumento de la capacidad de un capacitor debido a la presencia de un dieléctrico es lo que define la constante dieléctrica del material, que ya te anticipé en el capítulo de fuerza eléctrica y corresponde que repita acá: |
|
|
| CONSTANTE DIELECTRICA A 20 °C (εr) |
| Vacío |
1 |
| Aire seco (1 atm) |
1,00059 |
| Agua |
80 |
| Membrana plasmática (37 °C) |
8 |
| Papel |
3,5 |
| Plásticos |
3 – 20 |
| Vidrios |
5 – 10 |
|
|
|
| Campo eléctrico dentro del capacitor. El campo eléctrico dentro de los capacitores es uniforme y constante. Y se puede calcular fácilmente con esta fórmula: |
|
|
| |
|
|
donde σ es la densidad de carga, que se obtiene dividiendo la carga por el área en que está distribuida: σ = Q / A. Debido a la propia naturaleza de las cargas es muy raro que σ no sea una magnitud uniforme.
Si el espacio entre las placas está ocupado por algún material el campo se calculará dividiendo también por la constante dieléctrica del materia, εr. |
|
|
|
|
|
CHISMES IMPORTANTES: |
|
|
- Las membranas biológicas de todas las células (las nerviosas en especial) se comportan como capacitores. El impulso nervioso existe gracias a ello. Resulta que el interior y el exterior de las células poseen excesos de carga (negativas en el interior, positivas en el exterior). Esos excesos se acumulan sobre la membrana desesperados por pasar hacia el otro lado del compartimiento donde millones de cargas de signo opuesto los están llamando. El campo eléctrico que se genera dentro de ese aislante de grasa que es la bicapa lipídica y que tiene una constante dieléctrica de 8, resulta colosal.
|
|
|
- En cualquier artefacto electrónico hay cientos de capacitores (un índice de su relevancia); la gran mayoría se construye de la manera en que te los describí aquí, sólo que las placas metálicas son tan finitas que se pueden enrollar sobre sí mismas con un papel parafinado en el medio, como un sándwich. Los técnicos los llaman: capacitores de papel.
|
 |
|
|
| Los técnicos suelen decir faradio en lugar de faraday: eso es porque estudiaron con textos que traducen nombres propios, cosa que ahora parece ser correcta. |
|
- El faraday es una unidad de capacidad enorme. Prácticamente no existen capacitores de capacidad semejante. En general usamos subunidades del faraday como el nanofaraday, nF (10-9F), o el micofaraday, μF (10-6F), o a lo sumo el milifaraday, mF (10-3F), que se trata ya de un... bruto capacitor.
- Cuando comprás un capacitor en una casa de electrónica te lo venden
descargado. La carga que adquiera dependerá fundamentalmente de la fuente de potencial a la que lo conectes. Y además tenés que esperar un ratito para que se llene de cargas. En general traen indicada la diferencia de potencial máxima (y vos entonces podés calcular la carga máxima) que pueden soportar. Si lo conectás a una fuente de voltaje mayor lo más probable es que lo quemes y tengas que ir a comprar otro.
|
|
| PREGUNTAS CAPCIOSAS: |
|
 |
- En algunos manuales las unidades de εo en lugar de figurar como en todos lados: C²/Nm², figuran como F/m. ¿Podrás demostrar que estos grupos de unidades son equivalentes?
- ¿Cuánto vale la capacidad de una membrana biológica típica?
|
|
| |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-07. Buenos Aires, Argentina. |
|
|
 |
| | |
|
|

