 |
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA Y BIOFÍSICA
Ondas, generalidades
|
|

|
Ondas estacionarias I
|
|
Una onda estacionaria es una onda que parece quieta, que no viaja. Te explico de dónde surge, y después la definimos y caracterizamos con más precisión, ¿dale?
Las ondas estacionarias aparecen cuando en un mismo medio viajan dos ondas iguales pero con sentidos contrario: una va, la otra viene. |
|
|

|
|
|
Lejos de constituir una rareza de la física, es un fenómeno muy común... ya que es lo que ocurre normalmente cuando una onda cualquiera que viaja por un medio cualquiera, encuentra un obstáculo infranqueable y rebota conservando todas sus características, pero invirtiendo el sentido del movimiento.
El principio de superposición de ondas nos garantiza que al superponerse, resultará una nueva onda en la que las perturbaciones materiales serán la suma de las perturbaciones que produce cada onda por separado. Veamos qué pasa.
Dejemos momentáneamente de lado el asunto de la fase inicial para no complicarnos, después te cuento por qué en este caso son irrelevantes.
Las ecuaciones de las ondas serán: |
|
|
| onda que va |
y1(t,x) = A cos (ωt + kx) |
| onda que viene |
y2(t,x) = A cos (ωt – kx) |
|
|
|
ya que el signo del número de onda, k, es el que refleja el sentido de avance. De modo que la perturbacion resultante, ye, será la suma de las perturbaciones provocadas por cada una.
ye = y1 + y2
No tiene importancia cómo se resuelve el asunto. Se trata de una operación trigonométrica sencilla que vos podés resolver sin ayuda. Igual va una parte:
cos (a + b ) = cos a cos b – sen a sen b
cos (a – b ) = cos a cos b + sen a sen b
Si sumamos ambas expresiones llegaremos a lo siguiente (esta parte te la dejo como desafío)
cos (a + b ) + cos (a – b ) = 2 cos a cos b
O sea, en nuestro problema de las dos ondas viajeras iguales pero con sentidos contrarios, el resultado, ye, será: |
|
|
| |
ye(t,x) = 2A . cos ωt . cos kx |
|
|
|
|
Eso es lo que se llama ecuación de una onda estacionaria... y ya vas a ver por qué. A primera vista no parece muy diferente de la de las ondas viajeras... pero vamos a analizarla con un poco de detenimiento.
- Primero: sigue dependiendo del tiempo y la posición, como pasa en las ondas viajeras.
- Segundo: la amplitud de la onda resultante -la estacionaria-, es el doble de cualquiera de las ondas originales. Esto es perfectamente lógico ya que si dos ondas de amplitud A se superponen de alguna manera en todas las posiciones de un medio, será inevitable que en alguna posición, en algún instante, se superpongan totalmente y la amplitud valga 2A.
- Tercero: el factor cos kx es el que más caracteriza la onda estacionaria. Nos está diciendo que hay varias posiciones, xn, cuya perturbación será nula sin importar lo que digan los otros factores, o sea, en todo instante, o sea, SIEMPRE. (Acordate que cero por cualquier cosa es cero). Para todo x tal que kx valga pi (90°) o múltiplos de pi...
En una onda estacionaria existen posiciones fijas que parecieran no estar perturbadas: no se mosquean. Eso da la impresión de que la onda no viaja... y por eso se la llama onda estacionaria. |
|
|
 |
|
|
Las posiciones que arecen no estar perturbadas (y que, de hecho, no se mueven) reciben el nombre de nodo. El resto vientre... por motivos obvios. Algunos llaman antinodo a las posiciones de mayor amplitud (en el centro de los vientres).
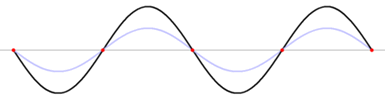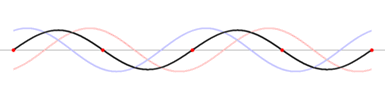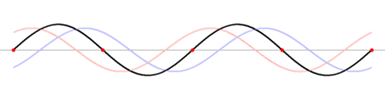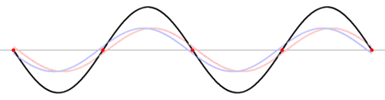
En este esquema te muestro siete instantes superpuestos de una onda estacionaria con ocho nodos (los extremos cuentan) y siete vientres.
Como podés apreciar a simple vista, la distancia entre 2 nodos es igual a media longitud de onda, λ. |
|
|
 |
|
|
Esta imagen (tomada de Wikipedia, http://en.wikipedia.org/wiki/Standing_wave) te muestra la formación de una onda estacionaria producida por dos viajeras idénticas: la representada en celeste que viaja hacia la derecha y la rosa hacia la izquierda. Tratá de verificar a ojo la función de suma.
Como el asunto de las ondas estacionarias es un poco largo -pero vale la pena- lo dividí en dos apuntes. No dejes de leer el siguiente. |
|
|
CHISMES IMPORTANTES |
|
|
- El mejor ejemplo de ondas estacionarias lo encontramos en las cuerdas de los instrumentos musicales. Los extremos de las cuerdas se hallan siempre fijos, de modo que las ondas que se establecen en ellas rebotan instalando ondas viajeras que viajan con sentidos opuestos. Al superponerse, aparecen las ondas estacionarias.
|
|
|
- La longitud de las cuerdas de los instrumentos musicales (y de cualquier otra cuerda en la que se establezca una onda estacionaria) mide exactamente media longitud de onda, λ/2; aunque -ya vas a ver- siempre hay escondidas ondas estacionarias de longitud de onda menor.
- La frecuencia con la que vibran las ondas estacionarias en las cuerdas depende de la velocidad de propagación de la onda en la cuerda. A su vez, esa velocidad depende de las características de la cuerda: cuán tensionada se halle, masa, grosor, etc.
|
 |
|
|
|
- La vibración en la cuerda también se contagia al aire circundante, en el que se establece una nueva onda -de tipo sonoro- que tiene la misma frecuencia que la onda en la cuerda (no podía ser de otro modo).
- Las ondas estacionarias siempre están confinadas en un medio (una cuerda, por ejemplo) que impone fuertes restricciones: los nodos no pueden ubicarse en cualquier lado. Eso le impone a las ondas viajeras que construyen la estacionaria estar siempre en fase. Aunque lo intentes, no pueden desfasarse.
|
|
 |
| PREGUNTAS CAPCIOSAS |
|
- ¿Cómo se llega a cos (a + b ) + cos (a – b ) = 2 cos a cos b?
- ¿La longitud de onda de la onda que vibra en una cuerda... es igual a la longitud de onda del sonido que produce al vibrar?
|
|
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización mar-09. Buenos Aires, Argentina. |
|
|
 |
 |
|
|
|

