|
NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA Y BIOFÍSICA
Ray optics
|
|

|
Reflection in Spherical Mirrors
|
|
This Esher drawing captures the curios deformation of images upon being refracted on spherical surfaces. But that which was born as a curiosity became immensely practical.
Mirrors which shrink the image but increase the visual campus are used as sideview mirrors for traffic. Mirrors which enlarge the image are used to fabricate telescopes. In this entry we shall focus on what these mirrors consist of, and how they function.
|

|
|
|
|
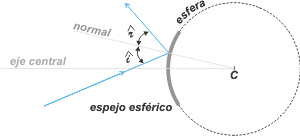
A portion of the sphere recieves the name spherical shell. If it is also mirrored we shall call it mirrored sphere. It may be mirrored through the external face, in wihch case it is called a convex sphere.
The center of the sphere, C, and the center of the mirror define a central axis or principal axis. |
|
|
|
The rays rebound fufilling the laws of reflection, that is, the angle of collision, i, and the angle of reflection, r, are equivalent.
The normal of the surface (whichever the point of collision may be) is a radius of the sphere. |
|
|
|
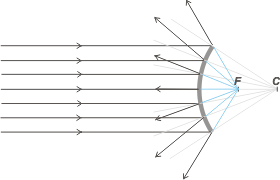
| Let use see what occurs when a beam of rays parallel to the central axis collide over the mirrored spherical surface. |
|
|
|
The rays rebound in every direction. Their prolongations towards the center of the sphere -all- pass through a point called the focal point, F, which is located half way between the mirror and the center, C.
That is: after rebounding, the light appears to eminate from the focal point! |
|
|
|
Of course, the inverse also occurs, a thing which is also known as the beginning of the reversibility of optical paths. |
|
|
|
|
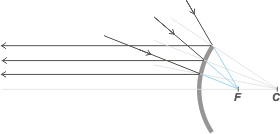
That is, any ray of light that collides over a spherical mirror and whos direction passes through the focal point F will be reflected in a direction parallel to the central axis C.
Knowing the paths of these pecular rays will be very important for finding the images. |
|
|
|
We shall examine now what occurs with a concave mirror, that is, a spherical shell mirrored on the inside. |
|
|
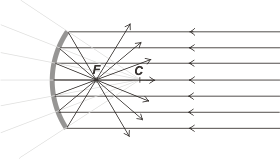
When a beam of parallel rays rebounds on a concave mirror the rays first concentrate on the focal point F, cross upon themselves, and then disperse in every dirrection.
Here too the focal point is found in the middle between the sphere and the center |
|
|
|
|
|
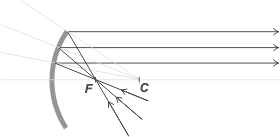
And, of course, due to the reversibility of optical paths: all rays that collide upon the mirror passing through the focal point rebound in a direction parallel to the central axis. |
|
|
Newly: any ray that collices over a spherical mirror whos direction passes through the focal point will be reflected in a direction parallel to the central axis.
Like the ones before, they are important rays due to the fact that their paths are easy to determine.
|
|
|
|
|
|
| In both cases (concave and convex mirrors) a ray which travels with the direction of the center of the sphere, C, will rebound upon itself (since it is normal in respect to the surface). |
|
|
| IMPORTANT GOSSIP |
|
|
-
Spherical mirrors tend to be circular (circular shells). Spherical is the form of the surface. And the border a circumference. The diameter of the circumference is called the aperture, D.
|
 |
- The spherical surfaces work well (that is: generate sharp images) if their aperture is sufficiently small with regards to the sphere it belongs. In practice sufficiently small means a tenth (F/D=10). That quotient is called focal relation.
|
- Mirrors with large apertures and low forcal relations are utilized in astronomy. They aren't spherical, but almost spherical. To construct them a spherical mirror is parted and slightly deformed (in jargon: it's shaped) until reaching a paraboloid of revolution
|
 |
|
|
 |
| PREGUNTAS CAPCIOSAS |
|
- Why is glass almost always used to manufacture mirrors?
- Why do some mirrors mirror from the back and others from the front?
- Can you prove geometrically that the radius of the sphere, r, is equal to twice the focal distance, f?
|
|
| |
| Translated by Nelson Bermudez-Bassett. Some Rights Reserved. Not allowed to be copied without naming either the author or this source material. Last updated apr-12. Buenos Aires, Argentina. |
|
|
 |
 |
|
|
|