NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
Teorema de Tales
Tales de Mileto nació en Mileto (hoy en Turquía) en el 625 a.C. Demostró varios teoremas, entre los cuales el más famoso (y útil) es el que voy a desarrollar aquí. Y que dice que: |
|

|
| Si tres o más paralelas son cortadas por dos transversales, los segmentos correspondientes resultan proporcionales |
|
|
|
Este gráfico clarifica el asunto: |
 |
|
p1, p2 y p3 son rectas paralelas. Las otras dos las cortan y no necesitan ser paralelas entre sí ni ortogonales con las paralelas, son transversales cualesquiera. Quedan definidos siete segmentos: AB, que se corresponde con el A'B', y BC, que se corresponde con el B'C'; También quedan definidos los segmentos AA', BB' y CC' de los cuales no nos vamos a ocupar (por ahora).
Todo lo anterior forma parte de la hipótesis. Y el teorema dice: |
|
| Vamos a la demostración. Para desarrollarla voy a utilizar el concepto de área de un triángulo: |
|
| Y para simplificar las cosas voy a trazar las transversales de forma tal que sean concurrentes en un punto perteneciente a una de las paralelas (en este caso C = C'): |
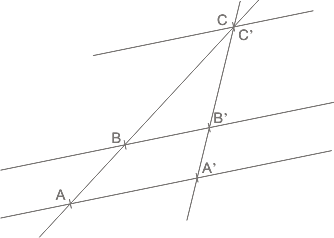 |
Luego bastará con desplazar lateralmente una de las transversales y ya quedamos en la formulación inicial.
A partir de acá vamos a trabajar con áreas, que denotaré de esta manera:
área del triángulo EFG =
aEFG
|
|
| Mirá los triángulos ABB' y BB'A'. Acá te los representé por separado: |
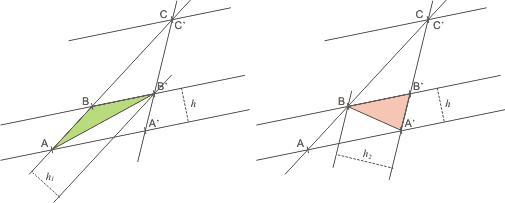 |
No cabe duda de que esos dos triángulos tienen el mismo área, ya que comparten la misma base, BB', y tienen la misma altura, h. Si esto te genera dudas podés consultarlo acá. En símbolos: aABB' = aBB'A'.
Pero cada una de esas áreas la podemos escribir en función de otro lado como base y su altura correspondiente. Así:
AB . h1 = A'B' . h2
(Obviamente, no escribí los 2 de los denominadores, cancelados).
Escrito de otro modo, queda así: |
|
| Con la ayuda de las mismas paralelas a las transversales que tracé las alturas h1 y h2, pordemos expresar el área del triángulo BCB': |
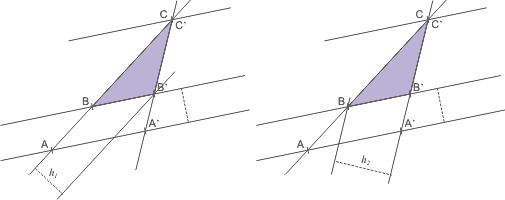 |
De modo que obtenemos:
BC . h1 = B'C' . h2
Escrito de otra manera: |
|
| Si igualamos las dos expresiones [1] y [2] que obtuvimos, llegamos al teorema. |
|
Que es lo que queríamos demostrar. Nos falta mover lateralmente la transversal que corrimos al principio. |
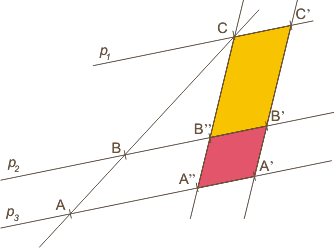 |
Como ves, las figuras que se forman entre paralelas son paralelogramos, una de cuyas características es que los lados opuestos son iguales, eso justifica que hayamos arrancado transladando una de las transversales.
Los segmentos determinados sobre las paralelas, también guardan cierta proporcionalidad... ¿te animás a escribirla?
También podés escuchar el Teorema de Tales cantado por Les Luthiers. |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-14. Buenos Aires, Argentina. |
|
| | | | |
| | | | |
| | | | |
|

