NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
Área de un triángulo
Todos los estudiantes recuerdan cómo hallar el área de un triángulo, basta con elegir uno de los lados como base, trazar la altura correspondiente, y entonces: |
|

|
|
|
No siempre reparan el el significado de la altura, h. Se trata del segmento que es perpendicular a la base y tiene extremos entre dos paralelas: una que contiene a la base y otra que contiene al otro punto del triángulo. |
 |
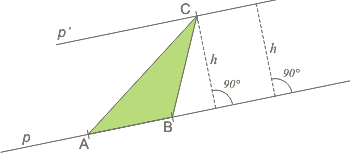 |
p y p' son dos rectas paralelas. Al segmento AB, uno de los lados del triángulo, fue tomado como base, y h es la altura correspondiente a esa base, que dibujé dos veces para que veas que no es necesario que pase por el punto opuesto, C. |
|
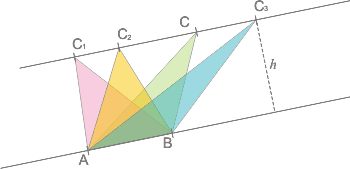
| Eso permite deducir que todos los triángulos que tengan la misma base y la misma altura tendrán el mismo área. |
 |
Si me permitís que simbolice el área del triángulo de esta manera:
aABC
entonces tenemos que:
aABC = aABC1
aABC1 = aABC2
aABC2 = aABC3 |
|
| Pero todavía no demostramos que el área de un triángulo deba calcularse de la manera conocida. No es difícil. Tomemos dos paralelas separadas un segmento h. |
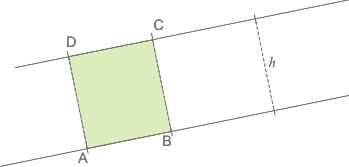 |
El área de ese rectángulo es lado por lado, o sea:
aABCD = AB . h |
|
| Si dividimos ese rectánculo con una de las diagonales, AC, el área de los dos triángulos que quedan determinados tendrán. cada uno, un área mitad que la del rectángulo. |
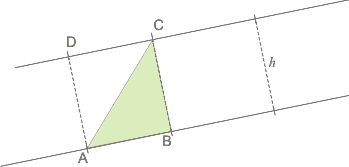 |
De modo que el área del triángulo nos queda: |
|
| Lo que vale para este triángulo rectángulo, también valdrá para cualquier otro triángulo mientras que tenga la misma altura. |
|
| Por lo tanto: |
| |
aABC = aABC1 = aABC2 = aABC3 = |
AB . h |
|
|
| 2 |
|
|
|
| Durante el desarrollo de los razonamientos utilicé al menos dos propiedades que, a su vez, requieren una demostración... aunque parezcan obvias, no son verdades absolutas. Una de ellas fue el asunto del área del rectángulo. ¿Te animás a descubrir cuál fue la otra? |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-14. Buenos Aires, Argentina. |
|
| | | | |
| | | | |
| | | | |
|

