NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
Teorema de Pitágoras
Acá va la tercera demostración. Esta es muy interesante porque aplica el criterio de semejanza de triángulos y se cree que es una de las demostraciones originales de Pitágoras.
Habíamos quedado que el buen señor dijo que en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos:
a² + b² = c²
|
|

|
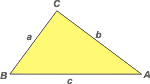 |
Donde a y b son las longitudes de los catetos y c es la longitud de la hipotenusa.
A los vértices opuestos a cada lado se les suele asignar el mismo nombre, pero en mayúscula.
En este ejemplo el ángulo recto es el correspondiente al vértice C. |
|
|
Bien. Tracemos una recta perpendicular a la hipotenusa que pase por el punto C. |
|
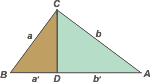 |
Al cortar a la hipotenusa la divide en dos segmentos, a'y b', que cumplen, obviamente: a' + b' = c.
Además, quedan formados dos triángulos nuevos: BCD y ADC. Ambos son rectángulos, eso salta a la vista... pero lo más importante es que ambos son semejantes al original ABC. |
|
|
Acá los tenés a los tres separaditos, para que puedas observar bien la semejanza: |
|
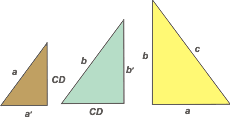 |
Si no te convence tu ojo, podés cerciorarte de que son semejantes deduciendo qué ángulos los forman. Tené en cuenta dos cosas: los ángulos interiores de todo triángulo suman 180° o, más sencillo todavía, los ángulos no rectos de un triángulo rectángulo siempre suman 90°; dos triángulos que tienen sus 3 ángulos iguales son semejantes. |
|
|
| La importancia de que sean semejantes pasa por lo siguiente: los lados correspondientes (también llamados homólogos) son proporcionales. Fijate, por ejemplo, qué pasa si comparamos el triángulo pequeñito (marrón) con el original (amarillo). |
|
| |
a |
= |
c |
La hipotenusa del chico dividida por el cateto menor del chico, es igual a la hipotenusa del grande dividido por el cateto menor del grande. |
|
|
| a' |
a |
|
|
Pongámoslo así:
a² = ca' [1]
De la misma manera, operando con el triángulo original y el celeste, llegamos a:
b² = cb' [2]
Ahora estamos listos para la parte central de la demostración. Mirá este dibujo: |
|
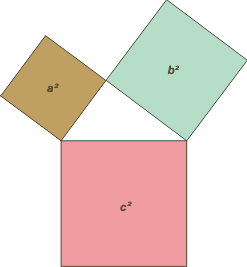 |
Acá dibujé un cuadrado sobre cada lado del triángulo. Cada cuadrado tiene de lado, el lado del triángulo sobre el que está apoyado.
El área de esos cuadrados vale (como todo cuadrado) lado por lado, o sea, a², b² y c², respectivamente.
|
|
|
| Tracemos la recta perpendicular a la hipotenusa que trazamos antes: |
|
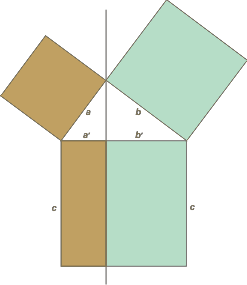 |
Acá encontramos que el cuadrado de abajo quedó dividido en dos rectángulos. Las áreas de esos rectángulos (base por altura) velen ca' y cb' respectivamente.
La suma de esas dos áreas es igual al área total del cuadrado de abajo.
ca' + cb' = c²
Si en esa expresión reemplazamos ca' y cb' por sus iguales que encontramos en [1] y [2], arribamos a lo que queríamos demostrar:
|
|
|
.
|
|
|
|
| |
|
| Si querés ver la primera demostración andá acá. |
|
¿Sabías? Euclides y Leonardo da Vinci también tienen demostraciones del teorema, que son bastante famosas. Y hasta un presidente de Estados Unidos halló una muy elegante. |
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-14. Buenos Aires, Argentina. |
|
| | | | |
| | | | |
| | | | |
|

