NO ME SALEN
EJERCICIOS RESUELTOS Y APUNTES DE FÍSICA Y BIOFÍSICA DEL CBC
Teorema de Pitágoras
Existen varias demostraciones del teorema de Pitágoras. Acá voy a desarrollar tres. Pero empecemos por definir al teorema.
Don Pitágoras dice que en todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos:
a² + b² = c²
|
|

|
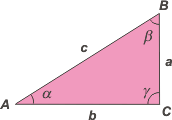 |
Donde a y b son las longitudes de los catetos y c es la longitud de la hipotenusa.
A los vértices opuestos a cada lado se les suele asignar el mismo nombre, pero en mayúscula.
Y al ángulo (interno) correspondiente, el mismo nombre que el vértice pero en su correspondiente del alfabeto griego. En nuestro caso α, β y γ. |
|
|
γ (gamma) es el ángulo recto (90°) de nuestro ejemplo.
Bien. Acá arranca nuestra domostración: |
|
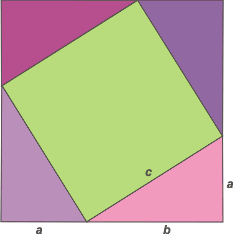 |
Dispongamos de cuatro triángulos rectángulos idénticos (les puse tonos rosa y fucsia) de esta manera, o sea, formando un cuadrado.
Fijate que el cuadrado formado tiene por lado la suma de los catetos de nuestros triángulos ( a + b ), y , además, en el centro se formó otro cuadrado, de lado c (que le puse un tono verde).
Sería muy justo que dudes de que la figura formada en el centro sea un cuadrado. |
|
|
Pero para sacarte la duda basta con que analices los 3 ángulos que parten del punto inferior al medio. |
|
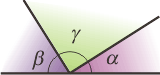 |
Si recordás la propiedad principalísima de los triángulos (cualesquiera) que la suma de los ángulos internos de un triángulo vale 2 rectos, 180°, un llano (mirá cuántas expresiones sinónimas), entonces, deberás aceptar que el ángulo del medio debe valer 90°.
Luego, si el cuadrilátero central tiene sus cuatro ángulos rectos y sus cuatro lados iguales, entonces, es un cuadrado. |
|
|
Bien, aceptado que el dibujo que nos quedó formado con los cuatro triángulos rectángulos idénticos es el que acordamos, entonces, el área de ese cuadrado grandote (el externo) es lado por lado, o sea: (a+b) x (a+b).
Pero también podemos expresar ese área como la suma de las áreas de los cuatro triángulos idénticos, más, el cuadrado interior de lado c (el verdecito).
El área de un triángulo -espero que lo recuerdes- es un medio de la base por la altura. En nuestros triángulos, si tomás el cateto a como base, la altura no es otro que b. Y si tomás a b como base, la altura no es otro que a. De modo que el área de cada triángulo vale ½ab.
Resumiendo:
( a + b )² = 4 ½ab + c²
Ahora un poquito de álgebra...
a² + 2ab + b² = 2ab + c²
Cancelamos los términos iguales y listo. |
|
|
|
| |
|
| Si querés ver la segunda demostración andá acá. |
|
¿Sabías? Antiguamente se llamaba teorema exclusivamente a la última proposición en un desarrollo lógico. Ahora se llama también al conjunto de las hipótesis, desarrollo (o sea, demostración) y conclusión. |
 |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-14. Buenos Aires, Argentina. |
|
| | | | |
| | | | |
| | | | |
|

