NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Vectores

|
|

|
| |
| DESCOMPOSICIÓN DE VECTORES
Para poder operar analíticamente con vectores (por ejemplo hacer sumas y restas) es apropiado previamente hacer una descomposición, en componentes paralelas a los ejes de un sistema de referencia, SR. El mejor modo de explicar qué significa todo esto es mostrar cómo se hace, paso a paso. Aquí va: |
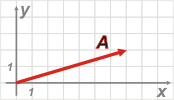 |
Supongamos que tenemos el vector A, que podría representar cualquier magnitud vectorial: una fuerza, una velocidad, una aceleración... Para descomponerlo necesitamos primero un sistema de referencia, x-y, que ya coloqué acá.
Por el extremo de A trazo rectas paralelas a los ejes del SR. |
|
|
|
| |
|
|
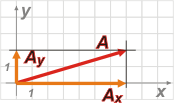 |
Cuando esas rectas cortan los ejes queda definido un punto (llamado coordenada) que es el extremo de los vectores componentes de A.
Entonces quedan definidas las componentes de A, también llamadas proyecciones de A sobre los ejes del SR. |
|
|
| En el ejemplo, el módulo de Ax vale 7 y el módulo de Ay vale 2. |
|
La componente de A sobre el eje x suele recibir el nombre Ax. Y la componente sobre el eje y, Ay.
Entre el vector original y sus componentes hay establecidas ciertas relaciones matemáticas, por ejemplo la relación pitagórica:
Ax² + Ay² = A²
Si te cabe duda de de dónde viene eso, prestale atención al triangulito sombreado: |
|
En el ejemplo, el módulo de A resulta valer 7,28 |
|
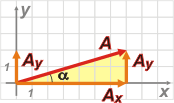 |
Y también deberás admitir que:
sen α = Ay / A
cos α = Ax / A
tg α = Ay / Ax
|
|
|
En el ejemplo, el valor de α resulta 16° |
|
Y lo más interesante que tienen las componentes es que (si recordás el asunto de la suma de vectores por el método de la poligonal o por el método del paralelogramo) la suma de las componente es igual al vector original.
Ax + Ay = A (¡Ojo! ¡esto que acabo de escribir es una suma vectorial!) O sea que la descomposición de vectores es la operación inversa de la suma. |
|
| Acá se ve qué importante sería contar con flechitas para colocar arriba de las letras... |
|
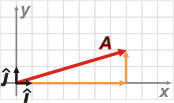 |
El broche de oro. Si para cada eje hubiéramos definido previamente un versor, entonces podríamos expresar lal vector A de esta manera:
A = 7 î + 2 ĵ
donde î y ĵ son los nombres habituales que reciben los versores de eje x e y respectivamente. |
|
|
|
| La combinación de estas dos operaciones (expresión con múltiplo de un versor y suma) nos ofrece un método apropiado para la operación analítica con vectores. |
|
|
| CHISMES IMPORTANTES: |
|
|
- Si los los ejes del sistema de referencia no fuesen ortogonales (es decir: no formasen 90° entre sí) no habría inconveniente en hacer descomposiciones y luego sumas o restas. Qué loca es la matemática.
|
|
 |
| ir derecho a la siguiente de vectores |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-09. Buenos Aires, Argentina. |
|
|
|

