NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Vectores

|
|

|
| |
| SUMA DE VECTORES, MÉTODO GRÁFICO
Para sumar gráficamente dos vectores hay dos métodos que, en el fondo, son el mismo método. El primero se llama método del paralelogramo. |
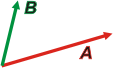 |
Consiste en colocar los dos vectores que se desean sumar en un mismo origen, luego construir un paralelogramo (un cuadrilátero que posee sus lados no consecutivos paralelos) tomando como lados los dos vectores. |
|
|
|
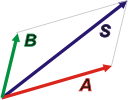 |
El vector suma es aquel que tiene origen en el mismo origen de los vectores que se suman y extremo en el vértice opuesto del paralelogramo. Coincide así, con una de las diagonales del paralelogramo.
A + B = S
|
|
|
|
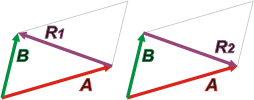 |
La otra diagonal se corresponde con la resta de los vectores. La resta no es conmutativa, con los vectores tampoco:
B – A = R1
A – B = R2
|
|
|
|
El segundo método de sumar vectores se llama método de la poligonal y consiste en dibujar un vector a continuación de otro: |
|
|
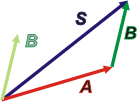 |
Lo que tiene de bueno el método de la poligonal es que se puede iterar repetidas veces sin mucha dificultad para sumar un número grande de vectores. El del paralelogramo es un poco más laborioso.
El vector suma, también suele llamarse resultante. |
|
|
|
| RESTA DE VECTORES
Si ya dominás analítica y geométricamente la suma de vectores, hacer la resta es bien sencillo, ya que restar M y S (elegí esos nombres por minuendo y sustraendo) es lo mismo que sumar M y –S:
M – S = M + (–S)
De modo que basta con multiplicar por -1 a un vector (o sea, invertirlo) para fabricar una resta a partir de una suma.
Sin embargo, como la resta entre vectores tiene una importancia especial, vamos a desarrollarla completamente y a destacar algunas propiedades importantes.
La principal es que la resta (tanto de los vectores como de los escalares) no es conmutativa. Para todo el mundo es fácil comprender que 5 – 3 no es lo mismo que 3 – 5. No es tan obvio con los vectores, pero es así: |
|
 |
 |
Una diagonal del paralelogramo que se forma con dos vectores cualesquiera se corresponde con la resta de los vectores. La resta no es conmutativa, con los vectores tampoco:
B – A = R1
A – B = R2
|
|
|
Probemos analíticamente el segundo caso:
A = Axî + Ay ĵ = 7 î + 2 ĵ
B = Bxî + By ĵ = î + 4 ĵ
|
|
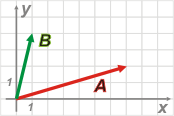 |
(Son los mismo que usé antes). |
|
|
Ahora restamos:
A – B = R2
A – B = ( 7 î + 2 ĵ ) – ( î + 4 ĵ )
A – B = 7 î + 2 ĵ – î – 4 ĵ
A – B = 6 î – 2 ĵ = R2
|
|
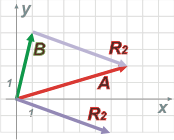 |
Y, como ves, su representación centrada en el origen es equivalente al vector que une los extremos de los vectores que se restan, con origen en el sustraendo y extremo en el minuendo.
Cuando los vectores que tengas que restar representen situaciones anteriores y posteriores (inicial y final) el sentido de la resta (si es R1 o R2) va cobrar sentido automáticamente. |
|
|
La suma sí es conmutativa, y es fácil ver (miralo en el gráfico de suma por el método del paralelogramo) que A + B = B + A = S. |
|
| CHISMES IMPORTANTES: |
|
- Si te cuesta resolver la resta, podes probar convertirla en una suma, que es más fácil. Por ejemplo, no sabés cuál de los sentidos (R1 o R2) es el correcto para resolver la resta A – B. Entonces te puede resultar más sencillo resolver la suma A + (–B). ¿Te cierra ahora?
|
|
| ir sin demoras al siguiente de vectores |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-09. Buenos Aires, Argentina. |
|
|
|

