NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |

|
19) Se tiene un recipiente de sección cuadrada mucho mayor que 1 cm², lleno de agua hasta
una altura de 2,8 m con una pequeña abertura de sección 1 cm² a 0,7 m de altura,
tapada por un corcho.
a) Calcular la presión manométrica sobre el corcho.
b) Si se extrae el corcho, calcular la velocidad de salida del líquido. |
| La primera parte del ejercicio es muy, pero muy sencilla. Se trata de una situación estática... hidrostática, que resolveremos, justamente, con el principio general de la hidrostática. |
|
|
|
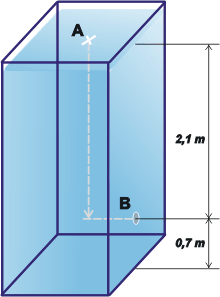
Tomemos dos puntos que nos van a servir para las dos partes del ejercicio: el punto A sobre la superficie libre del líquido y el punto B justo al lado del orificio (ahora tapado por el corcho).
ΔPr = ρ g Δy
Como nos piden la presión manométrica, eso significa que la presión en el punto A vale cero, y la diferencia de presión resulta ser la presión en B, la presión sobre la parte interna del corcho.
La diferencia de profundidad no es otra que la profundidad a la que se encuentra el corcho. Queda así:
prB = ρ g yB
|
|
|
|
prB = 1.000 kg/m³ . 10 m/s² . 2,1 m |
|
|
| |
|
|
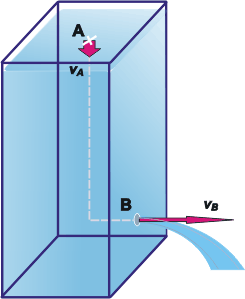
La segunda parte es claramente dinámica, porque el líquido comienza a fluir: se escapa velozmente por el orificio y desciende lentamente el nivel superior. Vamos a tener que aplicar el principio de Bernoulli.
prA + ρ g hA + ½ ρ vA² = prB + ρ g hB + ½ ρ vB²
|
|
|
|
Ahí aparece nuestra incógnita que es la velocidad del líquido en el agujero, vB. Y el resto parece interminable.
Pero puede resumirse bastante; por ejemplo: la presión en el punto B será -valga lo que valga- igual a la presión en A, ya que el líquido está en ambos lugares en contacto libre con la atmósfera y sometido exclusivamente a su presión; por lo tanto podemos cancelarlos.
La altura de B (ojo que Bernoulli habla de alturas, no de profundidades) podemos considerarla cero, y la de A, 2,1 m. Así vuela el término de la energía potencial de B.
Aún así, con lo hecho hasta ahora esta parte del ejercicio no saldría, ya que tenemos una sola ecuación y dos incógnitas, fijate: |
|
|
|
ρ g hA + ½ ρ vA² = ½ ρ vB²
Pero todavía podemos volar un término más ya que la velocidad con que desciende el líquido en el punto A es muy pequeña respecto al punto B. Para los expertos es lógico que esa gran diferencia autoriza la cancelación del término de energía cinética del punto A, pero supongo que vos te lo debés tomar como una trampa sucia de la peor calaña. Y que si a vos se te ocurriera hacer algo así en un examen te iniciarían juicio por difamación de la ciencia con tres años de prisión no excarcelable. Hagamos lo siguiente: por ahora creeme que se puede prescindir de ese término, y después de hallar el resultado, te lo voy a justificar. Entonces el asunto nos queda así:
ρ g hA = ½ ρ vB²
Suprimimos la densidad en ambos miembros y despejamos la velocidad de B.
vB² = 2 g hA
vB² = 2 . 10 m/s² . 2,1 m
|
|
la misma sucia trampa ya apareció en el ejercicio del sifón.
|
|
|
|
La deuda: el enunciado aclara que la sección del recipiente, SA, es mucho mayor que la de la abertura, SB. Haciendo una suposición austera, digamos unas 100 veces más grande. Si aplicamos el principio de continuidad entre esos dos puntos tenemos:
SA . vA = SB . vB
100 SB . vA = SB . vB
100 vA = vB
vA = vB / 100
Si incorporás esta relación a la ecuación de Bernoulli -cuando todavía no habíamos despreciado el término de la velocidad- nos va a quedar una única incógnita, vB, y el nuevo valor -calculalo- nos va a dar 6,48 m/s... creo que nos merecíamos ese permiso. |
|
|
|
|
|
| DESAFÍO:
Calcular la velocidad exacta de salida por el orificio si la sección del recipiente es apenas 50 veces más grande, nada más. |
|

|
| |
|
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización abr-08. Buenos Aires, Argentina.
|
|
| | |
|
|

![]()
![]()
![]()
