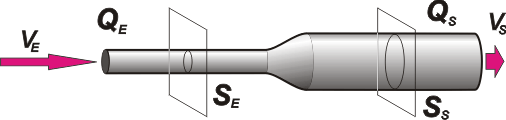
16) A non-viscous fluid flows through a horizontal pipe of varying cross-sectional area. Find the pressure variation between the pipe´s extremes in function of the entry velocity, v, and the density , ρ, if:
a) The exit area of the pipe is triple the entry’s area
b) The exit diameter is triple the entry´s diameter

Here another classic problem of energy conservation in a fluid (Bernoulli). Let´s go with the first part in which the exit area is triple the entry´s.

Written as an equation, the condition of this problem says:

S_S = 3 S_E

That has its consequence in the velocity, and in the velocity squared, given that:

Q_S = Q_E

S_S . v_S = S_E . v_E

3 S_E . v_S = S_E . v_E

3 v_S = v_E

And the squares:

9 v_S² = v_E²

v_S² = v_E² / 9

Now we can write Bernoulli´s equation (without the terms of potential energy, as everything happens at an equal height) to calculate the pressure variation, ΔP.

ΔP = ½ ρ (v_E² – v_S²)

ΔP = ½ ρ (v_E² – v_E²/ 9) = ½ ρ (8/9) v_E²

The new condition of this problem relates the pipes´ diameters, not their sections:

d_S = 3 d_E

d_S² = 9 d_E²

Yet, we can relate all the sections, remember that a circular section is  equal to S = (π/4) d²

(π/4) d_S² = 9 (π/4) d_E²

S_S = 9 S_E

This has a consequence in the velocity and in the velocity squared, as:

Q_S = Q_E

S_S . v_S = S_E . v_E

9 S_E . v_S = S_E . v_E

9 v_S = v_E

81 v_S² = v_E²

v_S² = v_E² / 81

Now we write  Bernoulli’s equation:

ΔP = ½ ρ (v_E² – v_S²)

ΔP = ½ ρ (v_E² – v_E²/ 81 ) = ½ ρ (80/81) v_E²

In both cases we face a pressure rise, owning to the fact that at the exit the velocity is less than at the entrance, and at an equal height, higher pressure regions have lower fluid speed.

CHALLENGE: What would be the pressure variation if the density of the fluid was 1.200 kg/m3 and the entry velocity 0,082 m/s?

Algunos derechos reservados. Se permite su reproducción citando la fuente. Traducción gentileza de Celina Nassello. Última actualización abr-08. Buenos Aires, Argentina.