| 
|
NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |
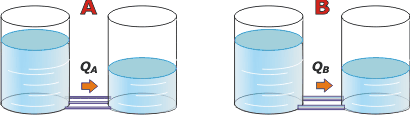
NMS 05* - Tres conductos horizontales, de igual longitud y área, conducen un fluido viscoso entre dos depósitos
que mantienen sus presiones constantes (ver figura). En esas condiciones circula un
caudal total de 24 lt/min. Si se reemplazan los tres conductos por otros dos,
de igual longitud pero de sección doble, ¿cuánto valdrá el caudal circulante en esas
condiciones (en lt/min)? |
|
|
Llamemos A la la situación inicial con 3 tubitos y 24 lt/min, y B a la segunda situación en la que hay 2 tubitos, pero más anchos, y un caudal, QB, que queremos averiguar.
Δpr = QA . RA
Δpr = QB . RB
A la diferencia de presión no le puse subíndice porque el enunciado aclara que se trata de los mismos tanques y en condiciones estacionarias. De modo que podemos igualar: |
|
|
|
|
|
QA es el caudal dato, y QB la incógnita. Si podemos establecer una relación numérica entre las resistencias hidrodinámicas para las dos situaciones podremos encontrar una relación numérica entre los dos caudales y decir cuánto vale QB.
Es posible encontrar la relación entre las resistencias... pero vamos por parte, porque es fácil perderse. Empecemos por las resistencias de los tubitos individuales.
La resistencia de 1 tubito sólo individual (mirá que hay 3) en el caso A, RiA, está dado por Poiseuille:
RiA = (8π) η l / SA2 resistencia individual de 1 tubito en el caso A
Donde SA es la sección de cada tubito individula del caso A. Y la resistencia conjunta de los 3 tubitos es la tercera parte (tres tubitos en paralelo tiene menos resistencia que un tubito solo). Si no te cierra ésto estás en la lona. Podés remontar esa parte acá.
RA = RiA /3
O lo que es lo mismo: |
|
|
|
|
|
De mismo modo se puede decir, para la situación B, que
RiB = (8π) η l / SB2 resistencia individual de 1 tubito en el caso B
RB = RiB /2
O lo que es lo mismo: |
|
|
|
|
|
Y para relacionar ambas situaciones hacemos uso del dato del enunciado que dice que la sección de los tubitos de reemplazo es el doble que los originales.
SB = 2 SA
Como nosotros vamos a necesitar usar cuadrados de secciones, elevamos esa igualdad al cuadrado y obtenemos:
SB2 = 4 SA2
Ahora metemos esta nueva igualdad en la expresión de la resistencia de 1 tubito B:
RiB = (8π) η l / SB2 = (8π) η l / 4 SA2
RiB = RiA /4
Las resistencias de los tubitos individuales las reemplazamos por sus respectivos equivalentes de resistencia conjunta, [2] y [3]:
2 RB = 3 RA /4
Finalmente, despejamos RA
RA = 8 RB /3
y lo metemos en la relación de caudales [1]:
QB . RB = QA . 8 RB /3
QB = QA . 8/3
QB = 24 lt/min . 8/3
|
|
|
|
|
|
Bueno, fue largo pero llegamos. Se trata de un ejercicio que tiene un 20% de física y un 80% de álgebra. Es un álgebra recontra sencilla... pero larga, tediosa y si no estás concentrado tenés muchas probabilidades de errarle. Este ejercicio, en el examen, lo respondió correctamente sólo un 15% de estudiantes. Por eso me pareció interesante resolverlo para todos, sobre todo para los futuros examinados.
Cuando tengas un nivel de experiencia algebraica aceptable, te va a parecer que el desarrollo que acabo de hacer es excesivamente puntilloso y abundante, que más de la mitad de los pasos los podías hacer en el aire sin escribir ni aclarar nada. Bueno, yo lo resolví como para los más iniciados. Pero no me cabe duda que los que lo resolvieron bien el día del parcial no tuvieron que escribir tanto. |
|
|
| *Ejercicio tomado en el examen parcial de Ciudad Universitaria en mayo de 2010. |
|
|
|
DESAFÍO: ¿Para obtener caudales iguales en ambas situaciones, el segundo caudal igual al inicial, habría que alargar o acortar los 2 tubos, y cuánto? |
|

|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización may-10. Buenos Aires, Argentina. |
|
|
| | |
|
|

![]()
![]()
![]()
