| 
|
NO ME SALEN
(PROBLEMAS RESUELTOS DE BIOFÍSICA DEL CBC)
FLUIDOS
|
|

|
| |
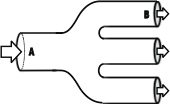
| NMS 01* - Un tubo de 4 cm² de sección transversal conduce líquido en régimen estacionario y se divide en 3 tubos iguales de 2 cm² de sección transversal cada uno. Todos los tubos están a igual altura y no hay efectos viscosos. Si P es la presión y v la velocidad: |
|
|
a) PA > PB vA < vB b) PA > PB vA > vB c) PA > PB vA = vB
d) PA < PB vA < vB e) PA = PB vA < vB f) PA < PB vA > vB |
|
|
| *Este ejercicio perteneció al primer examen parcial de Biofísica tomado en varias sedes del CBC simultáneamente el 3 de octubre de 2008. El porcentaje de respuestas correctas obtenidas entre 700 estudiantes rondaba el 40%. |
|
|
Este ejercicio es terriblemente fácil. Digo terriblemente porque la mayoría de los estudiantes que lo hicieron mal se agarraban la cabeza al comprender dónde habían metido la pata: todos aplicaron el principio de continuidad entre los tubos A y B. El error es grosero: suponete que por el tubo A ingresan 30 litros por minuto... ¿cuántos litros por minuto salen por B? Haber aplicado el principio de continuidad entre A y B, equivale a contestar que por B egresan los mismos 30 litros que entraron por A. Cuando lo obvio es que por B sale sólo la tercera parte, o sea 10 litros por minuto, ya que el ingreso se reparte por igual entre los tres tubos de salida.
Por otra parte, el ejercicio fue diseñado para resolverlo mentalmente y no tener que perder tiempo realizando cálculos. Te lo voy a resolver de tres maneras distintas: la primera es mi razonamiento sucinto, lo que habría hecho yo siendo examinado en el parcial. La segunda es el mismo razonamiento anterior pero desarrollado con las fórmulas y cálculos correspondientes. Y la tercera sería la forma tradicional, como lo haría una computadora que tiene cargadas las leyes que rigen el fenómeno físico y una creatividad nula.
RESOLUCIÓN EXPRESS: La sección total de salida es 6 cm², mayor que la de la entrada, que es 4 cm². Como a mayor sección menor velocidad, la velocidad en A debe ser mayor que en B. Por otro lado, no habiendo viscosidad ni diferencia de altura, y a mayor velocidad, menor presión... la presión en A debe ser menor que en B. STOP. Punto y a la bolsa. |
|
|
|
|
|
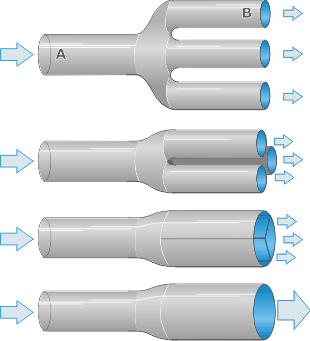
| RESOLUCIÓN EXPLICADA: Voy a aprovechar, acá, para tranquilizar a quien no sepa a qué se refiere la frase régimen estacionario que figura en el enunciado. Significa que no hay cambios en el tiempo. A veces tampoco resulta obvia la operación mental de la suma de las secciones que hice en la express. Armé esta secuencia de gráficos para explicarlo. |
|
|
|
Hacé de cuenta que la cañería es sumamente plástica y permite que dobles los tubos. Juntá lo más que puedas los tres caños de salida. Cuando estén totalmente juntos, los lados de las paredes -que quedaron como internas- podés retirarlos.
Ahora quedó un único tubo de salida, cilíndrico, cuya condición geométrica es que tiene la misma sección de salida que antes. O sea, la suma de las secciones de cada tubo de salida. Nuestro caso es muy sencillo, porque los tubos de salida originales eran todos iguales, de modo que la sección de salida total es 3 veces la sección de B. |
|
|
|
Este proceso lo tenés explicado con más detalle y para situaciones menos sencillas en este apunte.
Si llamamos T a la salida por ese caño de salida unificado, tenemos:
ST = 3 SB = 3 . 2 cm² = 6 cm²
Ahora sí, por continuidad:
QA = QT
SA . vA = ST . vT
4 cm² . vA = 6 cm² . vT
vA = 1,5 . vT
vA > vT
vA > vB
A los estudiantes que dudaban de que la velocidad con la que sale el líquido por el tubo unificado, vT, no fuese la misma que la del tubo finito original, vB, suelo proponerles la siguiente imagen. Suponete que un chico va caminando por la vereda a 10 km/h, y por la vereda de enfrente va una chica caminando a la misma velocidad, 10 km/h. De golpe se miran y se dan cuenta de que se aman y deciden seguir juntos para toda la vida. Entonces uno de ellos, cualquiera, cruza en diagonal, se dan un beso sin detenerse y continúan caminando juntos y felices tomados de la mano. ¿Ahora van a 20 km/h? ¿Tomarse las manos les imprime velocidad en las piernas?
Sigamos, por favor... Teníamos que vA > vB. Como no hay viscosidad, podemos aplicar la ley de conservación de la energía de Bernoulli (sin energía potencial):
PA + ½ ρ vA² = PB + ½ ρ vB²
Como el segundo término del primer miembro es mayor al segundo término del segundo miembro, no queda otra posibilidad que admitir que el primer término del primer miembro es menor que el primer término del segundo miembro. |
|
|
|
|
|
RESOLUCIÓN COMPUTADORA: La computadora aplica continuidad entre A y B. Pero reconoce que por B sólo sale la tercera parte de líquido que entra por A.
QA = 3 QB
SA . vA = 3 . (SB . vB )
4 cm² . vA = 3 . (2 cm² . vB )
4 cm² . vA = 6 cm² . vB
vA = 1,5 . vB
vA > vB
Ahora usa Bernoulli... y podría proceder de esta manera:
PA + ½ ρ vA² = PB + ½ ρ vB²
PA – PB = ½ ρ vB² – ½ ρ vA²
½ ρ ( vA² – vB² ) = PB – PA
El primer miembro es positivo, por lo tanto el segundo también lo ha de ser...
|
|
|
|
|
|
Si llegaste hasta el final, y tenés ganas de cerrar con una reflexión... opino que estudiar es hacer algo como lo que hicimos aquí: tomar un ejercicio y resolverlo de varias formas, una intuitiva, una formal, una personal, y relacionarlo con otras cosas vistas o aprendidas. Esta es, si se quiere, otra diferencia más entre una guía cualquiera de ejercicios resueltos y NO ME SALEN. |
|
|
DESAFÍO: Buscá algún razonamiento algebraico para reemplazar al de los chicos que caminan por la vereda. O sea, una explicación física de que las velocidades no se suman, sino que son iguales. |
|

|
| |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización oct-08. Buenos Aires, Argentina. |
|
|
| | |
|
|

![]()
![]()
![]()
