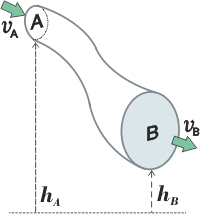
Todo estudiante o estudianta debe -al menos- darse cuenta de lo siguiente: acá hay un problema típico de conservación de energía (Bernoulli). Tal vez entre en la duda de si puede considerar al agua como un líquido ideal (ya que se sabe que el agua es un líquido levemente viscoso y su viscosidad vale 1 cp), y el enunciado no aclara. Pero en muchos caso (y este es uno de ellos) podemos considerar una buena aproximación a la realidad que el agua se comporta como un fluido ideal. De modo que comparemos las posiciones A y B.

Ahora vamos a la segunda pregunta. Tomemos h_B = 0. Ahora sí aplicamos el teorema de Berni.

pr_A + ρ g h_A + ½ ρ v_A² = pr_B + ½ ρ v_B²

y despejo pr_B

pr_B = pr_A + ρ g h_A + ½ ρ v_A² –½ ρ v_B²

pr_B = pr_A + ρ g h_A + ½ ρ (v_A² – v_B²)

Nunca, never, jamás... podés poner la excusa de que no conocés la densidad del agua.
Es lo mismo que decir que no sabés cuánto vale g.

pr_B = 152 kPa + 1.000 kg/m³ 10 m/s² 9,66 m + ½ 1.000 kg/m³ (5,18² – 2,86²) m/s

* En realidad el principio de continuidad puede aplicarse siempre que el fluido sea incompresible (densidad constante) como es el caso de casi todos los líquidos. No podés aplicarlo para los gases a menos que te indiquen que se mantiene constante la densidad. Y, por supuesto, si entre los puntos considerados hubiera fugas o aportes de fluido.

Para saber más: Acá un apunte teórico sobre el principio de Bernoulli.