NO ME SALEN
(LECCIONES TEORICAS DE BIOFÍSICA DEL CBC)
FLUIDOS
HIDRODINAMICA - PRINCIPIO DE BERNOULLI
|
|

|
| |
TEOREMA GENERAL DE LA HIDRODINAMICA
No está del todo claro si fue el padre, Johann Bernoulli (1667-1748) o el hijo, Daniel Bernoulli (1700-1782), el benefactor de la humanidad que descubrió la fórmula que –para evitar problemas familiares– llamamos simplemente Principio de Bernoulli.
Esta ecuación surge de la aplicación del principio de conservación de la energía mecánica, pero aplicada a un fluido. Por caso general tomemos una corriente en un tubo de ancho variable que además cambia de altura. En esta corriente de fluido ideal se cumple que
|
| pr + ρ g h + ½ ρ v² = cte. |
|
|
|
Analicemos por separado cada uno de los tres términos:
pr, el primero. pr es presión, y representa al trabajo que realiza sobre una masa de fluido, la masa de fluido de atrás que viene empujando. A este término se lo llama presión hidrodinámica. Proviene de dividir el trabajo de una fuerza exterior (L) sobre una masa de fluido, por su volumen (puse por en itálica porque se trata de una división, como cuando das una velocidad en kilómetros por hora).
ρ g h, el segundo. Densidad por gravedad por altura. Este término representa la energía potencial del fluido: la energía que posee simplemente por estar a cierta altura sobre la Tierra (recordá lo agradable que es ducharse en una casa cuyo tanque de agua está bien pero bien alto). A este término se lo llama presión hidrostática. Proviene de dividir la energía potencial gravitatoria de una masa cualquiera de fluido, m g h , por su volumen, algo así como una densidad de energía potencial.
½ ρ v², el tercero. Un medio por la densidad por la velocidad de la corriente al cuadrado. Este término representa la energía cinética del fluido. Proviene de dividir la energía cinética, ½ m v², por el volumen, algo así como una densidad de energía cinética.
Podrás concluir conmigo que el Principio de Bernoulli viene a ser algo así como el aspecto que el principio de conservación de la energía mecánica adopta en el barrio de los fluidos. Y a eso se llega dividiendo la energía mecánica del fluido por su volumen. Algo así como energía mecánica por unidad de volumen: la densidad de energía mecánica.
Acordate que la energía mecánica se conserva sólo cuando no hay fuerzas no conservativas actuando (LNC = ΔEM), de modo que el principio de Bernoulli sólo puede aplicarse a fluidos en los que la viscosidad (el rozamiento) sea despreciable. |
|
| los símbolos de presión p (pe minúscula) y de densidad, ρ (rho) se confunden estre sí, de modo que en No me salen usamremos pr para presión. |
|
| El principio de Bernoulli sólo se puede aplicar a fluidos ideales |
| |
|
Aún así representa una herramienta muy útil, y sumamente descriptiva.
Que la suma de los tres términos sea constante nos permite comparar dos estados, dos posiciones de una misma corriente:
prA + ρ g hA + ½ ρ vA² = prB + ρ g hB + ½ ρ vB²
|
|
|
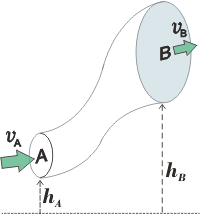
Acá tenemos una cañería en la que pueden variar las secciones y las alturas por las que circula.
Las alturas deben considerarse hasta el punto medio de la sección (en el esquema no lo indiqué así para ganar claridad) y el grosor del caño debe ser despreciable respecto a esa altura, si no... no vale.
Acordate que se trata de un fluido ideal con densidad constante y flujo ordenado. |
 |
|
|
|
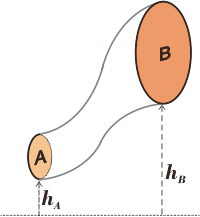
Veamos dos casos particulares y muy aleccionadores. Primero supongamos que el fluido está quieto (la canilla cerrada). En ese caso vA = vB = 0, los términos de energía cinética desaparecen y nos queda: |
|
|
prA + ρ g hA = prB + ρ g hB
reagrupando
ρ g hB – ρ g hA = prB – prA
ρ g (–Δh) = Δpr
que no es otra cosa que el principio general de la hidrostática. Si te lo olvidaste volvé acá. Ahí, fijate, hay una pequeñísima diferencia: en lugar de hablar de alturas hablé de profundidades... |
 |
|
|
|
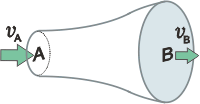
Ahora analicemos qué nos dice Bernoulli que pasa con una corriente horizontal, es decir, sin cambios de altura. Cuando hA es igual a hB, los segundos términos se cancelan y nos queda |
|
|
prA + ½ ρ vA² = prB + ½ ρ vB²
o sea: cuando la corriente va más rápido la presión es menor. Este resultado algunas veces parece contrario a nuestra intuición; sin embargo explica un montón de fenómenos interesantes como el vuelo de los aviones, el funcionamiento del calefón y, sobre todo, cómo hace la pelota para tomar comba en pleno vuelo y colarse en la red eludiendo la barrera. |
 |
|
|
|
CHISMES IMPORTANTES: |
|
|
- Parece ser que no alcanza con el efecto Bernoulli para sostener a los aviones. Si el asunto te interesa te invito a leer este brevísimo artículo que escribió mi amigo el Maestro Ciruela.
- Habrás notado que el calefón sabe cuándo está la canilla abierta y cuándo está cerrada. Un buen calefón, además, sabe cuándo está muy abierta y cuándo apenas abierta. En función de esto regula la llama del quemador que calienta el agua dentro del serpentín. Esta notable tarea la realiza utilizando la propiedad bernoulliana del cambio de presión con la velocidad: la sensibilidad al cambio de presión la tiene en una parte que se llama diafragma, que es la pieza que con más frecuencia hay que renovar en un calefón. El calefón sabe, la Biblia no.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|
|
- ¿Por qué un día de mucho viento, durante las ráfagas, se abren las ventanas mal cerradas?
- ¿Por qué en Quito, a 2.600 metros de altura, la pelota no toma efecto (no dobla en el aire) y los jugadores argentinos no pueden hacer esos magníficos goles de tiro libre?
- ¿Cómo funciona el calefón?
- ¿Qué es y cómo funciona un aerógrafo, o un tubo de flit?
|
|
 |
 |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización sep-07. Buenos Aires, Argentina. |
|
|
 |
|

