NO ME SALEN
(LECCIONES TEORICAS DE BIOFÍSICA DEL CBC)
FLUIDS
GASES
|
|

|
| |
Kinetic theory of gases
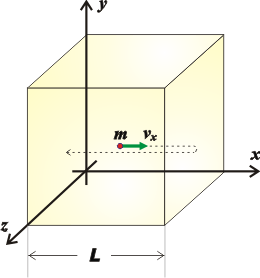
Microscopic study of gases (emphasizing the movement of individual molecules) allows establishing revealing relationships between matter properties. Let’s imagine a cube with side of L full of a simple gas (this means that all gas molecules are the same) in which we identify a single molecule of mass m, moving at a C speed, which is the average speed of all the gas molecules.
|
|
To simplify things, let's analyze the component of its velocity parallel to the x-axis. The molecule will collide with the two vertical walls perpendicular to the axis. And the force exerted by that molecule, f, on those two walls (some gas molecules move to the right and some to the left) can be described with Newton’s equation:
f = m ax
We say that Δt is the time that the molecule needs for travelling a length equal to that of the edge of the cube. Then, since it is a constant velocity:
vx = L / Δt y Δt = L / vx |
|
|
|
Where the force over the two walls will be:
f = m Δvx / Δt
Since collisions are elastic and the speed at each rebound changes in direction but not in sign, speed variation equals twice the speed itself:
f = m 2vx / Δt
If we replace the time interval with its equivalent according to the kinematics:
f = 2 m vx² / L
If we want to know the total force on these two faces, Fx , produced by all of the molecules , we just have to multiply that force by the number of molecules present in the cube, N.
Fx = N 2 m vx² / L
|
|
|
|
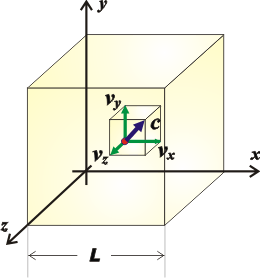
And if we want to know the value of the force on the six faces of the cube, we just have to add the force on the other two pairs of faces (which are going to be equal to the ones we already calculated). But thanks to Pythagoras, we can say that the sum of the squares of the components of a velocity equal to the square of the speed...
c² = vx² + vy² + vz²
Then, the total force on the 6 faces of the cube, F, would equal to:
F = N 2 m c² / L
|
|
|
|
If instead of being interested in forces, we are interested in a pressure , P, over the “walls” of the cube, we simply have to divide member by member by the total cube area 6L²
F / 6L² = 2 N m c² / 6L³
P = (1/3) N m c² / V
Or, (which is the same):
P V = (1/3) N m c²
It is convenient to multiply and divide the second member by two:
P V = (2/3) N ½ m c²
Where the last 3 factors are the average kinetic energy, ECm, of gas molecules: |
|
|
|
|
|
Then, we conclude that the product between gas pressure by its volume is a lineal function of its molecules’ kinetic energy.
An additional turn of the screw
If we reason that the number of molecules is equal to the product between the number of moles, n, by the number of Avogadro, No...
N = n No
and we replace it in the equation above...
P V = n (2/3) No ECm
And, if we also take in consideration the equation of state of the ideal gases...
P V = n RT
Where R is the ideal gas constant and T is the absolute temperature of the gas. Both have the same first member. We can make their second members match:
n (2/3) No ECm = n RT
|
|
|
|
|
|
Expression that sheds light on one of the emerging properties of matter: the temperature. What that final equation tells us is that the temperature is a macroscopic characteristic resulting from the sum of kinetic energies of the gas molecules. We could say: the microscopic explanation of a macroscopic phenomenon. |
|
|
| |
|
|
Curious Facts |
|
|
- The essential criticism that could be made to this explanation is that it considers that the molecules of the gas only collide with the walls of the cube and never with each other. True... So, the results shown here would approach more to reality the smaller are the molecules. That is one of the most important criteria to define what an ideal gas is (although there are more).
- This approach allows us to calculate the average speed at which the molecules of a certain gas move at a certain temperature. For example: 340 m/s for nitrogen at room temperature.
|
|
|
Captious Questions |
|

|
- Would you encourage to calculate the average stirring rate of the hydrogen gas molecules at room temperature?
- What could be Boltzmann's constant? (Do not confuse it with Stefan-Boltzmann's constant).
- Could this result have anything to do with the specific heat of the gases?
- If you take a container and you extract all the aire on it with a very powerful pump... What's the temperature inside of the container?
|
|
| |
|
|
| |
|
|
| Some rights reserved. Reproduction permitted if quoting the source. Last updated on Dec-16. Translated by Esteban Djeordjian. Buenos Aires, Argentina. |
|
|
|

| |
|
|
![]()
![]()
![]()