NO ME SALEN
(LECCIONES TEORICAS DE BIOFÍSICA DEL CBC)
FLUIDOS
GASES
|
|

|
| |
TEORÍA CINÉTICA DE LOS GASES
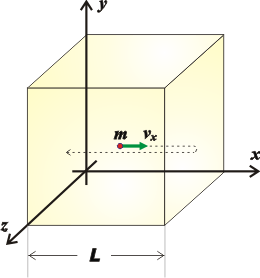
El estudio microscópico de los gases (abordando el movimiento de moléculas individuales) permite establecer relaciones reveladoras. Imaginemos un cubo de lado L lleno de un gas simple (o sea: todas sus moléculas iguales) en el que identificamos una única molécula de masa m, que se mueve con una velocidad c, que es la velocidad promedio con la que se mueven todas las moléculas del gas.
|
|
Para simplificar la cosa analicemos la componente de su velocidad paralela al eje x. La molécula chocará con las dos paredes verticales perpendiculares al eje. Y la fuerza ejercida por esa molécula, f, sobre esas dos paredes (algunas se mueven hacia la derecha y otras lo harán hacia la izquierda) se puede plantear con la ecuación de Newton:
f = m ax
Llamemos Δt al tiempo que tarda la molécula en recorrer una longitud igual a la de la arista del cubo. Entonces, como se trata de una velocidad constante:
vx = L / Δt y Δt = L / vx |
|
|
|
De donde la fuerza sobre las dos paredes será:
f = m Δvx / Δt
Como los choques son elásticos y la velocidad en cada rebote cambia de sentido pero no de signo, la variación de velocidad es igual a dos veces la misma velocidad.
f = m 2vx / Δt
Si reemplazamos el intervalo de tiempo por su equivalente según la cinemática:
f = 2 m vx² / L
Si queremos conocer la fuerza total sobre esas dos caras, Fx , producida por el conjunto de todas las moléculas, basta con multiplicar esa fuerza por el número de moléculas presentes en el cubo, N.
Fx = N 2 m vx² / L
|
|
|
|
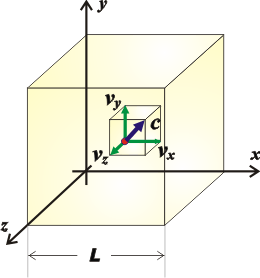
Y si queremos conocer el valor de la fuerza sobre las seis caras del cubo, basta con sumar la fuerza sobre los otros dos pares de caras (que van a ser iguales a la que ya calculamos). Pero la relación pitagórica indica que la suma de los cuadrados de las componentes de una velocidad es igual al cuadrado de la velocidad...
c² = vx² + vy² + vz²
Tendremos que la fuerza total sobre las 6 caras del cubo, F, será igual a:
F = N 2 m c² / L
|
|
|
|
Si en lugar de interesarnos en la fuerza nos interesamos en la presión, P, sobre las paredes del cubo, basta con dividir miembro a miembro por el área total del cubo, 6L²:
F / 6L² = 2 N m c² / 6L³
P = (1/3) N m c² / V
O, lo que es lo mismo:
P V = (1/3) N m c²
Resulta conveniente multiplicar y dividir por dos el segundo miembro:
P V = (2/3) N ½ m c²
Donde los últimos 3 factores no son otra cosa que la energía cinética promedio, ECm, de las moléculas del gas. |
|
|
|
|
|
Con lo que concluimos que el producto entre la presión de un gas por el volumen que ocupa es una función lineal de la energía cinética de sus moléculas.
Una vuelta más de tuerca
Si razonamos que el número de moléculas es igual al producto entre el número de moles, n, por el número de Avogadro, NA...
N = n NA
Y lo reemplazamos en la ecuación anterior...
P V = n (2/3) NA ECm
Y también recordamos la ecuación de estado de los gases ideales...
P V = n RT
En la que R es la constante de los gases ideales y T es la temperatura absoluta del gas. Ambas tienen el mismo primer miembro. Podemos igualar los segundos:
n (2/3) NA ECm = n RT
|
|
|
|
|
|
| Expresión que echa luz sobre una de las propiedades emergentes de la materia: la temperatura. Lo que nos dice esa ecuación final es que la temperatura es una característica macroscópica resultante de la suma de energías cinéticas de las moléculas del gas. Si se quiere: la explicación microscópica de un fenómeno macroscópico. |
|
|
| |
|
|
CHISMES IMPORTANTES |
|
|
- La principal crítica que se le puede hacer a este desarrollo es que considera que las moléculas del gas sólo chocan con las paredes del cubo y nunca entre sí. Es cierto. Por lo tanto este resultado se apartará menos de la realidad cuanto más pequeñás sean sus moléculas. Ese es uno de los criterios más importantes para definir lo que es un gas ideal (aunque hay más).
- Este planteo nos permite calcular la velocidad promedio a la que se mueven las moléculas de cierto gas a cierta temperatura. Por ejemplo: 340 m/s en el nitrógeno a temperatura ambiente.
|
|
|
| PREGUNTAS CAPCIOSAS |
|

|
- ¿Te animarás vos a calcular la velocidad promedio de agitación de las moléculas de gas hidrógeno a temperatura ambiente?
- ¿Que será la constante de Boltzmann? (No confundirla con la constante de Stefan-Boltzmann).
- ¿Podrá este resultado tener algo que ver con el calor específico de los gases?
- Si tomás un recipiente y hacés vacío con una bomba muy potente... ¿A qué temperatura queda el interior del recipiente?
|
|
| |
|
|
| |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización ago-13. Buenos Aires, Argentina. |
|
|
|

| |
|
|

![]()
![]()
![]()
