NO ME SALEN
(LECCIONES TEORICAS DE BIOFÍSICA DEL CBC)
FLUIDOS
HIDRODINAMICA - FLUIDOS VISCOSOS O REALES
|
|

|
| |
Ley de Ohm y ley de Poiseuille
RESISTENCIA HIDRODINAMICA
Ahora le toca el turno a los fluidos reales. Te voy a presentar dos nuevos conceptos con un ejemplo muy sencillo: imaginemos una jeringa cargada con agua primero y con dulce de leche después. En ambos casos queremos expulsar los líquidos lo más rápido posible. Con el agua no hay problema; un poco de fuerza y ya sale. Con el dulce de leche hay problemas: la fuerza que hay que hacer en el émbolo es grande, y aún así sale muy lentamente. Ahora lavemos bien la jeringa antes de guardarla (mentalmente) y analicemos la cuestión.
Queda claro que el nuevo fenómeno que aparece es el de la resistencia al movimiento del fluido. Como veremos esta resistencia es cuantificable, y por ahora la llamaremos simplemente R, resistencia hidrodinámica.
|
También resulta obvio que no todos los fluidos tienen la misma resistencia hidrodinámica. Y que cuanto mayor es ésta mayor tendrá que ser la fuerza que hagamos para empujarlo por la jeringa. En fluidos no hablamos de fuerzas sino de presión. Hasta ahora qué tenemos: que a mayor resistencia hidrodinámica mayor presión hay que hacer en el émbolo: ΔP es proporcional a R.
Si fuéramos capaces de hacer exactamente la misma fuerza en los dos casos (agua y dulce de leche), ¿cuál sería la diferencia? Lógico, a igual presión lo que cambiaría sería el caudal con el que sale cada fluido: el más resistente (el dulce), poco caudal y el menos resistente (el agua), mucho caudal. Entonces, R y Q son inversamente proporcionales.
Podemos juntar los dos razonamientos recontraintuitivos en una sola y sencilla ecuación: |
|
|
|
|
| |
|
A esta ecuación la llaman ley de Ohm hidrodinámica, por analogía con la ley de Ohm que se estudia en electrodinámica. Capaz que te diste cuenta que las proporcionalidades de las que hablamos en los razonamientos de entrada podrían no ser lineales. Sin embargo -por suerte- la cuantificación de los hechos da así. |
|
|
Existe una fuerte analogía entre la corriente de fluidos y la corriente eléctrica. Tan fuerte es que las ecuaciones que describen ambos fenómenos son casi las mismas. Cambian algunos nombres y, por consiguiente, algunos símbolos. Pero las ecuaciones funcionan de la misma manera. |
|
|
|
¿En qué unidades debe medirse la resistencia hidrodinámica? Según la ley de Ohm hidrodinámica, queda claro que las unidades de resistencia deben ser iguales a las unidades de presión divididas por las unidades de caudal. En el sistema internacional
|
|
|
| [R] = |
|
[ΔP] |
= |
Pa |
= |
Pa.s |
= Pa.s.m-3 = Pa.s/m3 |
|
|
|
|
| [Q] |
m3 |
m3 |
|
| s |
|
|
|
Te las escribí de todas las maneras posibles.
Ahora bien, de qué depende la resistencia hidrodinámica. Supongamos que tenemos que desagotar un tanque de agua. La tarea será más rápida si lo hacemos por un caño grueso que por uno finito, y también por uno corto que por uno largo. Parece obvio que la resistencia aumente cuanto más finito y más largo sea el tubo. ¡Ah! Y también depende del tipo de fluido que esté circulando (agua, dulce de leche, aceite, aire...)
La propiedad de los fluidos que tiene que ver con su resistencia a circular por un caño o por donde sea se llama (ya lo habíamos dicho) viscosidad, que se simboliza con la letra griega minúscula terrorista eta, η. Resumamos todo en una ecuación: |
|
|
|
|
|
que se llama ecuación o ley de Poiseuille, en honor al médico fisiólogo francés Jean Louis Marie Poiseuille (1799-1869), que llegó a esta ecuación interesado en las características del flujo de la sangre. Recordando que la sección transversal de un tubo cilíndrico: S = π r², la misma ley puede escribirse así: |
|
|
|
|
|
El primer factor, 8/π u 8π -según el caso-, es una constante numérica que no debe preocuparte para nada, y que tiene que ver con la geometría cilíndrica de los tubos, caños y mangueras y con el modo en que circula el fluido (laminar); luego aparece la viscosidad, η, la longitud del caño, l, y el radio de la sección, r. La potencia cuarta indica que la resistencia hidrodinámica es fuertemente sensible al radio del tubo. Una pequeña diferencia de diámetro de un caño implicará una gran diferencia de su resistencia hidrodinámica.
¿En qué unidades se mide la viscosidad? De la ley de Poiseuille se desprende fácilmente que las unidades en las que debe medirse la viscosidad deben ser las mismas que las de la resistencia hidrodinámica por las de longitud a la cuarta potencia divididas las de longitud (8 y pi son números, no tienen unidades). |
|
|
| [η] = |
|
[R] . [r4] |
= |
Pa.s . m4 |
= Pa.s |
|
|
|
| [l] |
m3. m |
|
|
|
De modo que la viscosidad se medirá en pascal segundo.
Aquí te pongo un cuadro con algunas substancias famosas y sus viscosidades. |
|
|
Valores típicos de viscosidad en pascales por segundo (Pa.s) |
Agua (0°C) |
1,792 x 10-3 |
Agua (20°C) |
1,005 x 10-3 |
Aire (20°C) |
1,9 x 10-5 |
Sangre (37°C) |
4 x 10-3 (*) |
Plasma (20°C) |
1,81 x 10-3 |
Aceite para automotor (SAE 30) |
2,3 x 10-2 |
*La viscosidad de la sangre puede variar por diversos factores fisiológicos, como el nivel de oxigenación, cantidad de glóbulos rojos, etc. Los valores normales varían entre 1,5 x 10-3 y 5 x 10-3. |
|
|
|
| Una conclusión inmediata de la ley de Ohm hidrodinámica es que un fluido viscoso que avanza por una cañería horizontal va perdiendo presión, por el sólo hecho de avanzar. Existe una experiencia sencilla que pone al descubierto este efecto importantísimo. Consiste en colocar a lo largo de un caño horizontal pequeños tubitos verticales, abiertos por arriba y espaciados uniformemente (se llaman piezómetros). Como el fluido que avanza lo hace con cierta presión, al encontrar la vía de escape ascenderá, pero sólo hasta cierto nivel (en el que la presión hidrostática en la parte inferior del tubito iguale la presión hidrodinámica dentro del caño)... y mirá lo que ocurre: |
|
|

|
|
|
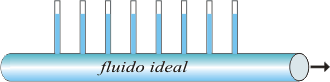
| Si se tratase de un fluido ideal, en cambio, los tubitos de arriba marcarían todos el mismo nivel, indicando que circula sin pérdida de presión, sin pérdida de energía. Mirá ahora la diferencia si el fluido fuese ideal: |
|
|
|
|
|
CHISMES IMPORTANTES: |
|
|
- El saber popular confunde viscosidad con densidad. Cree que son la misma cosa o que por lo menos van de la mano: "a mayor densidad mayor viscosidad" y viceversa. Y en verdad son propiedades que describen cosas totalmente diferentes y además son absolutamente independientes. El aceite de máquina, por ejemplo, es menos denso que el agua y varias veces más viscoso. El mercurio es 13 veces más denso que el agua y sin embargo a 0°C es un poco menos viscoso.
- Los expertos en materiales dicen (créanlo o no) que el vidrio es un fluido, en especial, un líquido, que parece sólido simplemente porque su viscosidad es altísima. Parece ser que se han encontrado relojes antiquísimos cuyos vidrios vistos de canto, están adelgazados en la parte superior y engordados en la inferior, o sea, tomando la forma de una gota. Cuando se mira la estructura atómica del vidrio con un microscopio electrónico se ve que efectivamente parece un líquido detenido en el tiempo.
|
|
|
| PREGUNTAS CAPCIOSAS: |
|

|
- Si la viscosidad es algo equivalente al rozamiento, ¿por qué se lubrican las máquinas con líquidos muy viscosos, como los aceites, y no con líquidos menos viscosos, como el agua?
|
|
| |
|
|
| |
|
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización sep-07. Buenos Aires, Argentina. |
|
|

|
| | |
|
|

![]()
![]()
![]()
