NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
 |
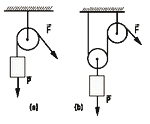
NMS s2.09 - Hallar la intensidad de la fuerza que se
debe realizar para mantener en equilibrio un paquete
que pesa 120 kgf en los siguientes casos. |
 |
 |
|
Estas cosas se llaman poleas y aparejos. Para analizarlas a todas vamos a tener en cuenta que las cuerdas del CBC (las cuerdas ideales) realizan la misma fuerza en toda su extensión, en particular en sus dos extremos.
Empecemos con la polea simple, caso (a). En este caso la polea tiene la ínica utilidad de desviar la dirección de la soga o, para lo que a nosotros nos interesa, desviar la dirección de la tensión, T, que no es otra que F. |
|
|
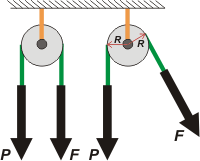
Miremos el DCL correspondiente. Sobre la polea actúan (acá y siempre) tres fuerzas. Dos las ejerce la soga y son iguales. La tercera que actúa sobre el eje de la polea y en este caso se dirige hacia arriba (no necesariamente vertical) no la representé como un vector porque en este caso no nos interesa, termina soportándola el techo, que suele ser todo lo robusto que se necesite.
El hecho de que F y P se ejercen sobre los extremos de una misma soga garantiza que ambas son iguales. |
 |
|
|
| No afecta para nada que una de ellas, F, cambie de dirección. Si analizamos el caso de la derecha vemos que el momento que cada una realiza sobre el eje de la polea tiene el mismo módulo. Concluyendo: |
|
| |
F = P en nuestro caso: F = 120 kgf |
(a) |
|
|
| Vamos al caso (b), polea móvil. Al tirar de la cuerda la polea que sostiene la carga sube o baja, por eso recibe su nombre. Es la que está en el medio, va un esquema. |
|
La de arriba de todo no cuenta para nada es una pole fija que hace la tarea más sencilla, pero no modifica el valor de la carga, como vimos en lo anterior.
En la que le sigue, que es la nuestra, aparecen nuevamente 3 fuerzas, las dos que tiran para arriba las hace la cuerda, o sea, F. Y la que tira para abajo es el peso de la carga que deseamos sostener (levantar o bajar, pero en equilibrio). Si le pedimos consejo a Newton nos va a decir:
2F — P = 0
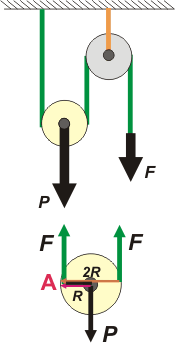
A quien le gusta ver el problema desde el punto de vista del cuerpo extenso (DCL inferior). Como la cuerda está a atada en un extremo al techo se la puede ver como un apoyo. Consideremos a A ese punto de apoyo, luego los momentos de P y F son diferentes. La distancia desde el apoyo hasta P vale R, y hasta F, 2R. Quien lo mira de este modo ve en la polea móvil una palanca del mismo estilo que la carretilla. De cualquiera de las dos maneras obtenemos. |
 |
|
|
| |
F = P / 2 en nuestro caso: F = 60 kgf |
(b) |
|
|
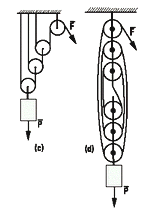
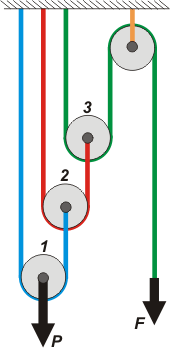
| Ahora viene el arreglo (c), aparejo potencial. Como siempre tememos la polea de arriba que facilita las cosas pero no modifica la carga. Y luego aparecen 3 (podrían aparecer n) poleas móviles enganchadas sucesivamente. |
|
Tal vez te percates que no son igual de móviles (la de abajo se desplaza menos que la de arriba), pero eso es un detalle, no te preocupes. Lo que sí es relevante es que el aparejo éste funciona con cuerdas diferentes, y cada cuerda hace una fuerza diferente al resto.
Para remarcar esa condición importante te dibujé cada cuerda de un color diferente (no fue por una reminiscencia de mi jardín de infantes). Las fuerzas que hacen las diferentes cuerdas las voy a llamar así: cuerda azul, TA, cuerda roja, TR , y cuerda verde, lógicamente, F.
Veamos qué pasa polea por polea. En la 1
2TA = P
en la polea 2
2TR= TA
y en la 3
2F = TR
|
 |
|
|
Combinamos las tres ecuaciones (es un juego de niños) y nos queda:
2 . (2 . (2 . F)) = P
|
|
| |
F = P / 2n en nuestro caso: F = 15 kgf |
(c) |
|
|
Y ahora viene las estrella de la ingeniería, el aparejo factorial. Es el más popular de todos y se usa mucho en la industria y la navegación. Generalmente es el peor interpretado por los estudiantes, y no es culpa de ustedes. Las explicaciones (sobre todo las representaciones gráficas) suelen ser deficientes. Si lo quieren hacer sencillo introducen cuerdas que se doblan (?) como en nuestra guía, o aparejos con poleas de tamaños diferentes que no se ven en ninguna parte más que en los libros de física, y todos meten fuerza irreales entre las poleas que complican la situación. Yo te lo voy a plantear diferente. Primero te voy a mostrar el esquema que hice yo. Es de tipo realista, es el que los otros autores le huyen porque al lector se le arma un bollo de cuerdas en el que se queda enredado. Pero yo te tengo fe. Y además te voy a hacer una propuesta muy, pero muy práctica.
Primero mirá el esquema. Te lo hice en tres partes, rotándolo de a poco para que lo puedas ver por alrededor. Me llevó 1 hora hacerlo. Dedicale 1 minuto. |
|
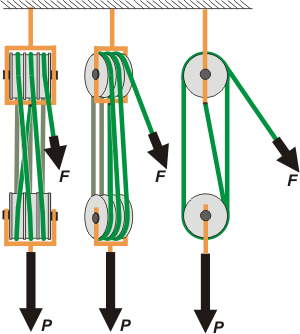 |
Como ves tiene una sola cuerda, que se enhebra varias veces por cada conjunto de poleas. La fuerza que hace esa cuerda, no es otra que F, la que tendrá que hacer el operario (o el navegante).
Hay dos conjuntos de poleas. Suelen ser idénticos. Las de arriba juegan el papel de poleas fijas, y ya sabés qué hacen y qué no hacen.
El conjunto de abajo es el que interesa. Las poleas que lo forman juegan el rol de las poleas móviles y ahí está el secreto. Para resolverlo tengo un método muy sencillo. Me parece que es original, porque no recuerdo haberlo visto nunca. |
|
|
| Te propongo que mires solamente el aparejo inferior. Acá te agrego un DCL propio para que no te confundas |
|
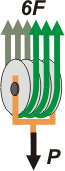
Ok, ahí está. Ahora consideralo (no es demasiado imaginativo lo que te pido) un cuerpo único, sólido, bonito... y eso sí, de masa despreciable, como siempre. Y contestame sin titubear: ¿no son seis los trozos de cuerda que salen hacia arriba? ¡Claro! Dos por cada polea del conjunto. Seis cuerdas, igual a 6 F. ¿Y para abajo? ¡Una sola! la carga que queremos sostener, o sea P. ¿Qué diría Newton en este caso? Newton diría...
6 F — P = 0
Un ingeniero, en cambio, lo diría así: |
 |
|
|
| |
F = P / 2n en nuestro caso: F = 20 kgf |
(d) |
|
|
| Me parece que era demasiado fácil. |
|
| |
|
| Comentario: Las poleas son viejísimas, pero fue Arquímedes, alrededor del 250 AC, el que se dio cuenta de que combinándolas de diferentes maneras se lograban multiplicadores de fuerzas sumamente útiles. Fue él quien le dio el nombre -aparejos- a estos montajes, y se cuenta la historia de que logró levantar una embarcación de varias toneladas y botarla al mar utilizando solo la fuerza de sus músculos. |
|
|
| DESAFIO: Disponés de seis aparejos de 2 poleas cada uno. Si contás con todas las cuerdas que necesites y todos los ganchos en el techo que sean necesarios, ¿Cómo armarías un dispositivo de izado que requiera el menor esfuerzo posible? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

