NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
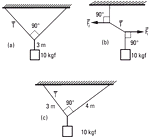
FIS s1.08- a- Indicar en qué casos puede ser calculada la tensión T, si sólo están dadas las cantidades que se indican en las figuras. Considerar: F1 = F2.
En el caso en que la información sea insuficiente, indicar qué dato es necesario para poder
resolver el problema.
No te alarmes, abajo están las figuras más grandes. |
 |
|
Interesante ejercicio. Arranquemos con el caso a): |
|
|
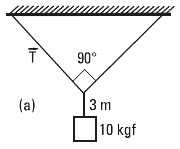 |
Lamentablemente no hay cómo calcular la tensión. Si las cuerdas oblicuas tuvieran la misma longitud (como sugiere el dibujo), entonces, sí, se prodría calcular, de hecho, ya lo hicimos en el ejercicio anterior, 1.7.
En este caso resultaría:
T = 10 kgf / 2 cos 45°
T = 7,07 kgf
Los 3 metros de la cuerda de abajo salen sobrando, no aportan nada a los fines del cálculo. |
|
|
| |
falta algún otro ángulo o longitud
de las cuerdas oblicuas |
a- |
|
|
| Vamos al b-. |
|
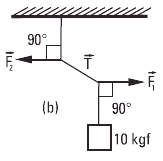 |
Para el que tiene buen ojo (y casi seguro que eligió ingeniería civil) es obvio que el valor de T no puede obtenerse ya que depende de la inclinación de esa cuerda.
Si estuviese vertical cuando F1 = F2 = 0, haría una fuerza de 10 kgf; y su valor crecería (¡hasta el infinito!) cuando se pone más oblicua al crecer las fuerzas laterles.
Pero intentemos una demostración analítica: |
|
|
Planteemos el equiibrio en ambos nudos:
F1 = T cos α
10 kgf = T sen α
F2 = T cos α
10 kgf = T sen α
Sin conocer el valor de las fuerzas o sin conocer α el sistema no tiene solución. Si querés probar no me opongo. (No son 4 ecuaciones, son sólo dos, ya que hay dos pares iguales entre sí, y las incógnitas son 3). |
|
| |
No se puede, hace falta conocer la geometría del sistema |
b- |
|
|
| Vamos al c-. |
|
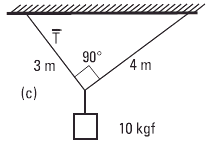 |
Este es más complicado... no anticipemos nada. Planteemos el equilibrio del nudo. Usemos un sistema de referncia x horizontal e y vertical, y llamemos T' a la fuerza que hace la soga de la derecha.
T cos α = T' cos β
10 kgf = T sen α + T' sen β
|
|
|
α (el ángulo entre la cuerda de la izquierda y el techo) y β (entre la cuerda de la derecha y el techo) se pueden conocer gracias a los datos de las longitudes de las cuerdas oblicuas: el triángulo que forman con el techo es rectángulo (dato aportado por la figura), donde la línea del techo que une los puntos de suspensión es la hipotenusa y las cuerdas son los catetos. Entonces:
tg α = 4 m / 3 m
tg β = 3 m / 4 m
De donde α = 53° y β = 37°
Con esta información nos vamos a las ecuaciones y resolvemos.
T 0,6 = T' 0,8
10 kgf = T 0,8 + T' 0,6
Podemos despejar T' de la primera:
T' = T 0,75
Y eso lo metemos en la segunda:
10 kgf = T 0,8 + T 0,75 . 0,6
10 kgf = T 1,25
|
|
|
|
| Se pudo. |
|
| |
| DESAFIO: ¿Cuánto vale el máximo largo que puede tener la cuerda que hace la fuerza T' del ítem c- sin aflojarse? |
|
 |
Algunos derechos reservados.
Se permite su reproducción citando la fuente. Se agradece a Gunter Bonwit, Diego Sandoval y Eduardo Flores por el envío de unas erratas. Última actualización oct-16. Buenos Aires, Argentina.
|
|
|

