NO ME SALEN
(EJERCICIOS RESUELTOS Y APUNTES TEÓRICOS DE FÍSICA)
Estática
|
|

|
| |
FIS s1.07-Tres cables A, B y C atados a único nudo se
mantienen tirantes y en equilibrio. Las tensiones
de los cables A y B son de 45 kgf cada una.
Calcular la tensión del cable C, en los siguientes casos:
a- A y B son paralelos.
b- A y B son perpendiculares.
|
|
|
|
|
Acá hay una pequeña ambigüedad: cuando nos dicen que los cables A y B son paralelos no nos dicen si tiran para el mismo lado o para lados opuestos. En el caso en que tiren para lados opuestos no cabe duda de que se equilibran mutuamente, ya que tienen el mismo módulo. Luego la tensión del cable C debe ser nula.
Si en cambio tiran para el mismo lado, es obvio que la tensión del cable C debe ser igual a la suma de los otros dos. (No pienso hacer álgebra para esto). |
|
|
|
| Más interesante es el ítem b-. vamos a hacer un DCL. |
|
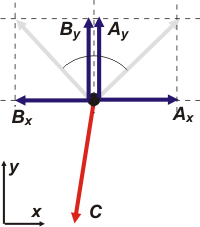 |
Acá lo tenés.Las tensiones que hacen los cables A y B ya los reemplacé por sus componentes en el SR que elegí arbitrariamente.
Seguramente estás alarmado porque representé al cable C inclinado hacia la izquierda, y vos ya sabés que eso está mal. En realidad lo que estaría mal sería dibujarlo bien, porque esa propiedad debe surgir de la resolución del ejercicio. No pocas veces cometemos ese error de anticipar (¡y a veces erradamente!) propiedades que no tenemos que usar y que surgen de nuestras creencias, representaciones, intuiciones, alucinaciones... y que, en todo caso, debemos demostrar o refutar. |
|
|
Bueno, como elegí un SR bisectriz entre las cuerdas A y B... sus componentes quedan así:
Ax = A cos 45° = 45 kgf cos 0,707 = 31,8 kgf
Ay = A sen 45° = 45 kgf cos 0,707 = 31,8 kgf
Bx = B cos 45° = 45 kgf cos 0,707 = 31,8 kgf
By = B sen 45° = 45 kgf cos 0,707 = 31,8 kgf
Ahora puedo plantear la sumatoria de fuerzas, igualada a 0 si agrego a C, como equilibrante:
Ax — Bx — Cx = 0
Ay + By — Cy = 0
De la primera ecuación surge claramente que Cx = 0, o sea: el cable C no hace fuerzas laterales respecto al eje elegido, o sea, la bisectriz entre los cables A y B.
Y de la segunda ecuación, entonces, surge su módulo. |
|
| |
|
| |
|
| |
| DESAFIO: ¿Te animás a graficar C en función del ángulo de separación de las fuerzas? |
|
 |
| |
Algunos derechos reservados.
Agradezco a Florencia Rocío Aragona por el envío de una errata. Se permite su reproducción citando la fuente. Última actualización mar-16. Buenos Aires, Argentina.
|
|
|

