NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
 |
Adicional 39- Un baúl de 80 kg es transportado en un camión
volcador. Para bajar el baúl, el camionero inclina
la caja del volcador, hasta que observa que éste comienza a moverse. Hallar qué distancia recorre
el baúl sobre la caja inclinada, sabiendo que
los coeficientes de rozamiento entre el baúl y la
caja son μe = 0,75; μd = 0,25, y que el baúl abandona
la caja con una velocidad de 4 m/s. |
| Nota: Resolver este problema por consideraciones
dinámicas y también por consideraciones
energéticas. |
|
La resolución por consideraciones de dinámica es tediosa pero sencilla. Arranquemos, como siempre, con un DCL, en este caso nos describe ese instante crucial en el que el baúl comienza a deslizar. Se trata de una situación límite... o sea, te conviene imaginar que todavía no está deslizando... pero que si el camionero inclina la caja del camión una millonésima de grado más... |
|
|
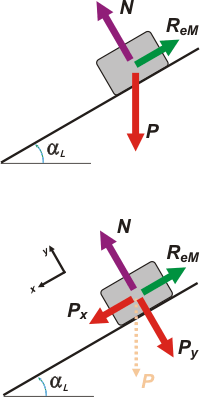 |
Este de acá arriba es el DCL puro: nos indica las fuerzas que están actuando sobre el baúl en esa situación límite.
La fuerza con que lo atrae la Tierra, el peso, P. La fuerza con que lo apoya el piso inclinado del camión, N. Y la fuerza de rozamiento estática que también le hace el piso del camión y es la responsable de que no deslice... y como está a punto de soltarlo ya que el camionero está decidido a expulsar el baúl: se trata de la fuerza de rozamiento estático máxima, ReM. Y no hay más fuerzas.
Para poder operar algebraicamente con esos vectores voy a necesitar hacer alguna descomposición vectorial, y así obtener vectores codireccionales únicamente. Lo más práctico es descomponer la fuerza peso en dos direcciones -una paralela y otra normal al piso del camión-, y lo mejor indicado para los estudiantes iniciados es hacer un segundo DCL que dé cuenta de esta decisión.
La trigonometría indica que:
Px = P . sen αL
Py = P . cos αL
|
|
|
|
Ahora aplicamos la Segunda Ley de la dinámica por separado para cada eje.
Px — ReM = 0
N — PY = 0
Y podemos recordar que la naturaleza de las fuerzas de rozamiento nos indica que
ReM = μe . N
En esta última ecuación podemos reemplazar las dos anteriores
Px = μe . PY
P . sen αL = μe . P . cos αL
sen αL = μe . cos αL
μe = tg αL
αL = arc tg μe (no lo calcules... contenete)
Con esto averiguamos el ángulo de inclinación con que el baúl arranca su viaje de descenso. Con ese mismo ángulo baja y sale disparado a una velocidad de 4 m/s. Esta nueva situación dinámica es muy parecida a la anterior. |
|
|
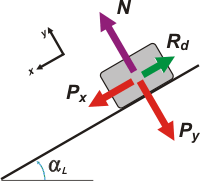 |
La única diferencia es que la fuerza de rozamiento es de tipo dinámico y -por lo tanto- menor.
Vamos a las ecuaciones de Newton más la de rozamiento:
Px — Rd = m . a
N — PY = 0
Rd = μd . N
|
|
|
|
reemplacemos la segunda en la tercera y la tercera en la primera:
Px — μd . PY= m . a
P . sen αL — μd . P . cos αL = m . a
m . g . sen αL — μd . m . g . cos αL = m . a
g . sen αL — μd . g . cos αL = a
a = g . (sen αL — μd . cos αL) (no lo calcules... contenete)
Para hallar la distancia recorrida sobre la caja inclinada tenés que hacer un poquito de cinemática (espero que no te hayas olvidado).
d = ½ a Δt²
vF = a Δt
Ahí tenés dos ecuaciones con dos incógnitas: la distancia recorrida sobre la caja, d, y la duración del viaje, Δt. La velocidad final, vF, es dato del ejercicio y la aceleración puede ser que no sepas cuánto vale -si lograste contenerte- pero sabés que se puede calcular en base a los datos del ejercicio. Resolvamos: de la segunda despejo Δt y lo que da lo reemplazo en la primera. Queda ésto:
d = vF² / 2a (ahora sí calculo)
|
|
|
| |
d = 2 m |
(fue un parto, pero llegamos) |
|
|
|
Vamos a la resolución que apela a las consideraciones energéticas:
WFnc = ΔEM
La única fuerza no conservativa que actúa durante la bajada es la de rozamiento.
WRd = EMF — EMO
El rozamiento y el desplazamiento forman 180º. La energía mecánica inicial es puramente potencial, y la final puramente cinética (si tomo como nivel igual a cero la posición en la que el baúl sale de la caja).
— μd . d . m . g . cos αL = ½ . m . vF² — m . g . hO
La altura inicial es igual a d. sen αL...
— μd . d . m . g . cos αL = ½ . m . vF² — m . g . d. sen αL
— μd . d . g . cos αL = ½ . vF² — g . d. sen αL
d . g . sen αL — μd . d . g . cos αL = ½ . vF²
d . g ( sen αL — μd . cos αL) = ½ . vF²
d = vF² / 2 g ( sen αL — μd . cos αL)
|
|
|
| |
d = 2 m |
(¡uy! ¡da lo mismo!) |
|
|
|
Varios pasos que me salteé en este último desarrollo no hay más remedio que calcularlos haciendo consideraciones dinámicas, por ejemplo, el cálculo del ángulo de inclinación, o la fuerza de rozamiento.
Si te sirve para revisar tus cálculos, el ángulo vale 36,86º y la aceleración 4 m/s². |
|
 |
| DESAFIO: Después de hiciste este ejercicio... no me da el cuero para desafiarte. |
|
| Algunos derechos reservados.
Se prohibe terminantemente imprimir en blanco y negro y sin citar al autor que sigue tomando mate. Última actualización mar-08. Buenos Aires, Argentina. |
|
|

