NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
Adicional No me salen E4* -Un esquiador de 80 kg se deja deslizar desde la
parte superior de una ladera de 60 m de alto y
que forma con la horizontal un ángulo de 37º, al
llegar al pie de la misma se sigue deslizando
sobre la pista horizontal. Si el coeficiente de
fricción entre los esquíes y la nieve es de μd = 0.2 y el esquiador no se impulsa durante el
recorrido, determinar la distancia sobre la pista que recorre el esquiador hasta detenerse.
|
Este ejercicio es el súper clásico de los que los profes llaman: disipativos, porque la energía que ande dando vueltas por cualquier parte del problema termina disipándose -en este caso- por la fuerza de rozamiento (que es la arquetipo de la fuerzas disipativas).
Se presenta en dos versiones: una tonta, en la que el rozamiento sólo se presenta en la parte horizontal; y otra más razonable en la que el rozamiento actúa durante todo el trayecto. Voy a resolverte ambos, empezando por el tonto. Va el esquema: |
|
|
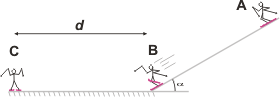 |
Espero que el dibujo sea de tu agrado. Lo importante es que los sucesos de los cuales hablen las ecuaciones o el texto tengan nombre (y lo más práctico es nombrarlos con una letra).
Apliquemos esta ley de conservación: |
|
|
|
ΔEMAC = WFnc
EMC — EMA = WFnc
Tal vez te sorprendas de que no compare energéticamente A con B y en cambio lo haga entre A y C. El motivo es que el teorema es válido para cualquier par de estados... no necesitan ser correlativos ni consecutivos. Nada pide el enunciado sobre el suceso B, pues, lo mejor es ignorarlo.
La Energía mecánica en A es puramente potencial, ya que la velocidad en A vale cero (está dicho, aunque sutilmente, en el enunciado). Si tomamos el cero de las alturas en el nivel del tramo horizontal, entonces, la energía mecánica en C valdrá cero, ya ahí el esquiador se detiene. Por otro lado la única fuerza no-conservativa que actúa en la transformación A-C es el rozamiento que hay en la pista horizontal, cuyo trabajo podemos calcular con la definición de trabajo para fuerzas constantes. Tenés que tener presentes algunas cuestiones de las fuerzas de rozamiento (te recomiendo darle un repasito al problema 2.3 de dinámica en el que un ladrillo desliza del mismo modo que nuestro esquiador aquí. Entonces tenemos:
0 — EMA = WRoz
— m g hA = Roz d cos 180º
— m g hA = — μd m g d
hA = μd d
d = hA / μd
|
|
|
| |
d = 300 m |
(aplausos, vítores) |
|
|
|
Antes de pasar a lo importante fijate un par de cosas. Primero: el resultado fue independiente de la masa del esquiador. Segundo: el resultado tiene sentido lógico, la distancia será mayor si el tío se lanza desde más arriba, y será menor cuanto mayor sea el rozamiento.
Bueno, ahora vamos al problema más interesante y más aproximado a la realidad, o sea: esquíes y nieve rozan por igual ya sea en la montaña como en la pista. Por otro lado es la interpretación correcta del enunciado del ejercicio. |
|
|
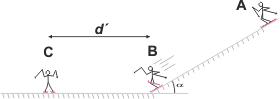 |
La mayor parte de las consideraciones que hice en el planteo previo valen también para éste. La única diferencia es que el trabajo del rozamiento -a los efectos del cálculo- vamos a dividirlo en dos tramos: el inclinado y el horizontal.
Entonces: |
|
|
|
ΔEMAC = WFnc
EMC — EMA = WFncBC + WFncAB
0 — m g hA = — μd N d´ — μd N´ L
¡Atenti! Pará un cacho: la "normal" (o mejor dicho: la fuerza de apoyo en la nieve) no vale lo mismo en cada tramo, y por ello la fuerza de rozamiento tampoco. Si se te complica verlo dentro de tu cabeza te recomiendo mirarlo en el problema 2.16 de dinámica en el que teníamos justamente un esquiador deslizando con rozamiento en una ladera de montaña, no me acuerdo si de Bariloche o Las Leñas.
N´= m g cos α
Por otro lado la longitud de la ladera -que ya te habrás dado cuenta que llamé L- se puede expresar en función de la altura de A y el ángulo de inclinación:
L = hA / sen α
meto estas dos consideraciones en la ecuación de energía...
— m g hA = — μd m g d´ — μd m g cos α hA / sen α
hA = μd d´ + μd cos α hA / sen α
hA — μd cos α hA / sen α = μd d´
d´ = ( hA / μd) — (hA cos α / sen α)
|
|
|
| |
d´ = 220 m |
(aplausos, ovación) |
|
|
|
Mirá, no te lo pierdas: este resultado es coherente con el anterior. Surge de restarle a los 300 m de antes una cantidad que tiene que ver con la altura y el ángulo de inclinación. La dependencia con la inclinación te la da la expresión cos α / sen α. No es difícil de analizar. Si te resulta de utilidad, podés buscar su igual cot α. |
|
|
| DESAFIO: Calcular la energía cinética del esquiador en la posición B en ambos planteos (con y sin rozamiento en la pendiente) |
|
 |
| |
| *Este problema me lo envió Vanina Fagre, estudiante de la UTN. |
|
| |
|
| Algunos derechos reservados.
Se prohibe terminantemente imprimir en blanco y negro y sin citar al autor que sigue tomando mate. Última actualización jun-07. Buenos Aires, Argentina. |
|
|

