NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
 |
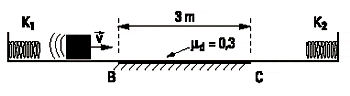
2.21- Un cuerpo de 4 kg es impulsado por un
resorte de constante elástica k1= 6400 N/m por
una pista horizontal en la que el rozamiento es
despreciable, salvo en la zona BC donde el coeficiente
respectivo es µd = 0,3; rebota contra otro
resorte de constante k2, e ingresa nuevamente a
la zona con rozamiento, deteniéndose exactamente
en el punto B. Hallar: |
|
a- La compresión inicial máxima del resorte
de constante k1.
b- La constante elástica del otro resorte, sabiendo
que ambos sufrieron idéntica compresión
máxima.
c- En qué punto se detendrá al repetir la experiencia
con las mismas condiciones iniciales,
sustituyendo el resorte 2 por otro con una constante
13 veces mayor.
|
Escuchá esto: un matrimonio de jardineros que está trabajando en un jardín, cortando tallos... el marido le dice: "Seamos felices, mientras podamos" ¡Jua, jua, jua! ¿Lo entendiste...? "mientras podamos". Ok, ok, ya sé, no tiene nada que ver... preferís este problema que es un plomazo. (Podamos... no puede ser...)
Te lo repito una vez más... para aplicar el método (ojo que me puse serio) de leyes de conservación tenés que tener en claro (¡y a tu lector también le tiene que quedar claro!) qué eventos estás comparando. Te voy a hacer una secuencia de todos los sucesos notables por los que vamos a ir pasando y le voy a poner nombre a cada uno de ellos (si no le ponemos nombres a las cosas de las que nos referimos, es imposible entenderse). Acá va: |
|
|
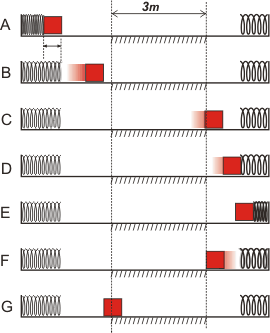 |
El resorte 1 comprimido un cierto Δx empuja al cuerpo, que adquiere una velocidad entra al tramo con rozamiento, sale de él con una velocidad menor, comprime al resorte 2. Te cuentan que esa compresión es igual a la del 1 al principio. El cuerpo rebota, vuelve a entrar al tramo con rozamiento. ahora en el sentido opuesto y se le acaba la cuerda justo cuando estaba por salir del rozamiento.
A cada evento le puse un nombre y podría haber destacado más... pero de todos éstos ya hay varios que sobran, no importa.
Tenés que tener en cuenta, además, algunas otras cositas. Por ejemplo, que durante la pasada por el tramo con rozamiento, el |
|
|
|
sentido del desplazamiento y el sentido de la fuerza de rozamiento son opuestos (sus vectores representativos forman 180 grados. Eso ocurre tanto cuando el cuerpo va para un lado como cuando va para el otro. La longitud del tramo, BC, es dato y vale 3 m. (A BC le tendria que poner una rayita arriba -segmento BC- pero en HTML es un despiole).
Y lo más importante a tener en cuenta es que el método de leyes de conservación te permite comparar dos eventos cualesquiera, no necesitás que sean consecutivos, ni siquiera cercanos. Por ejemplo, para responder la primer pregunta del enunciado voy a comparar directamente los eventos A y G (!)
WFncAG = ΔEMAG
WFncAG = EMG — EMA
El primer término te está pidiendo que sumes todos los trabajos de todas las fuerzas no-conservativas que hayan actuado entre A y G. La única (ya no hace falta que repasemos todas) es la de rozamiento y su trabajo en cada paso es
WRoz = — μe m g BC
como entre A y G se realizan dos trabajos de esos:
WFncAG = — 2 μe m g BC
eso es lo que vale el primer miembro de la ecuación inicial. Sigamos con el segundo término. Acordate que energía mecánica es la suma de la cinética más la potencial gravitatoria más la potencial elástica.
— 2 μe m g BC = ECG + EPgG + EPeG — ECA — EPgA — EPeA
si tomamos altura igual a cero en el nivel en el que ocurre todo el problema, las energías potenciales gravitatorias valdrán cero. (Y si elegimos otro cero igual se cancelan, porque serán iguales). La cienética de A y de G también valen cero. Lo mismo la elástica de G. ¿Qué queda?
— 2 μe m g BC = — ½ k1 ΔxA²
2 . 0,3 . 4 kg . 10 m/s² . 3 m = ½ . 6.400 N/m . ΔxA²
La única incógnita era ΔxA, o sea, lo que nos pedían. Despejala y listo. |
|
|
|
|
|
Para responder la segunda pregunta comparo A con E. Siempre del mismo modo (ya voy más rápido, ¿sí?)
WFncAE = ΔEMAE
— μe m g BC = ½ k2 ΔxA² — ½ k1 ΔxE²
acordate que ΔxA = ΔxE, entonces sólo nos falta k2 |
|
|
|
|
|
| Para la última pregunta no hace falta hacer ninguna cuenta. Fijate que entre el evento C y el F no actúa ninguna fuerza no-conservativa. Sea cual sea el elástico que coloques en la posición del 2 (mientras sea un elástico ideal como los del CBC) su trabajo será conservativo, y no modificará la energía mecánica del cuerpo, por lo tanto se va a detener en el mismo lugar que donde se detiene ahora. |
|
|
| |
v = 0 en el punto B |
"podamos, podamos..." ¿lo entendiste? |
|
|
|
| |
|
|
| DISCUSION: La lección importante de este ejercicio es que el método energético puede aplicarse para comparar cualquier PAR (siempre de a dos) de eventos, incluyendo en el primer miembro todos los trabajos de las fuerzas no conservativas que haya ocurrido durante esas dos situaciones. Quienes no conocen esta potencialidad pierden mucho tiempo calculando variables (alturas, posiciones, velocidades, estiramientos, etc., etc.) intermedios, cuando en realidad pueden ir directo a la caza de la incógnita que les interesa tomando el evento que lo incluye como estado en la comparación. |
|
 |
| DESAFIO: Acá tenés un desafío con una lección importantísima. Hacela y si no te sale en 5 minutos es porque no cazaste la idea que te quiero mostrar (no es la misma idea que discutí arriba, es otra cosa). Si no te sale consultalo con tu docente... porque, ya te digo, es súper importante. Si en cada pasaje por el tramo con rozamiento el cuerpo pierde 36 J, ¿dónde se detendrá (en qué lugar exacto) si el resorte 1 le confiere una energía inicial de 894 J? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Leer con moderación. Prohibida su venta a menores de 18 años. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

