NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, energía mecánica)
|
|

|
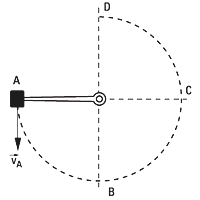
2.16 - Una varilla rígida de masa despreciable
y de 80 cm de longitud puede girar en un plano
vertical, alrededor de un eje horizontal que pasa
por uno de sus extremos, mientras que al otro
extremo está fijo un contrapeso de 2 kg. El contrapeso
es lanzado hacia abajo, desde la posición
A indicada en la figura.
|
a- Determinar el vector velocidad en el punto
A, si al girar con rozamiento despreciable la varilla
se detuvo en posición vertical D.
b- Determinar qué fuerza ejerce la varilla sobre
el contrapeso, cuando éste pasa por las posiciones
B, C y D, en ese caso.
c- El contrapeso se lanza desde el punto A con
la misma velocidad que antes, pero ahora el rozamiento
en el eje hace que la varilla se detenga
en posición horizontal. Determinar el trabajo realizado
por las fuerzas de rozamiento en el recorrido
AC. |
 |
|
Lo importante antes de resolver este ejercicio es darse cuenta de que no hay ninguna fuerza no conservativa actuando. El eje al cual está unida la varilla le permite girar libremente, no le comunica ninguna fuerza de rotación, sólo la sostiene, ¿está claro?
Si es así, ya podés anticipar que el trabajo de todas las fuerzas no conservativas en cualquier intervalo considerado, será nulo.
WFnc0A = 0
Y, por lo tanto, la energía mecánica del contrapeso valdrá lo mismo en cualquier instante y en cualquier posición. Comparemos las energías mecánicas en A y en D.
EMA = EMD
ECA + EPA = ECD + EPD
½ m vA² + m g hA = ½ m vD² + m g hD
Fijate que como energías potenciales sólo puse las potenciales gravitatorias, ya que al no haber resortes o elásticos unidos al contrapeso, no puede tener energía potencial elástica. Por otro lado podemos tirar la energía cinética en D, ya que es un dato del enunciado que la velocidad en ese punto vale cero. Y por último podemos tomar el cero de las alturas en la posición de A (hA = 0), con lo cual su energía potencial se anula y la altura de D resulta igual al largo de la varilla, L.
½ m vA² = m g L
½ vA² = g L
vA = ( 2 g L )½
vA = ( 2 . 10 m/s² . 0,8 m)½
|
|
|
|
|
|
Vamos a la pregunta siguiente: b- Determinar qué fuerza ejerce la varilla sobre
el contrapeso, cuando éste pasa por las posiciones
B, C y D, en ese caso. Tené presente que la varilla no puede hacer sobre el contrapeso fuerzas laterales, solo puede hacer fuerzas que tengan la misma dirección que la varilla, ya sea hacia afuera o hacia adentro.
En los tres casos la respuesta nos la va a dar la dinámica (se trata de un movimiento circular) a través de la Ley de Newton. La aceleración centrípeta la voy a expresar en los tres casos como: ac = v² / r = v² / L . Acá van los 3 casos. |
|
|
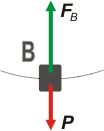 |
Primero tenemos que conocer la velocidad con la que pasa por B.
EMA = EMB
ECA + EPA = ECB + EPB
½ m vA² + m g hA = ½ m vB² + m g hB
Tomemos el cero de las alturas en el mismo lugar que antes. Y cancelemos la masa. |
|
|
|
½ vA² = ½ vB² — g L
Acordate que vA² = 2 g L, entonces:
vB² = 4 g L
Ahora sí, vamos a Newton:
ΣF = m acB
FB — P = m vB²/ L
FB = m g + m 4 g L / L
FB = m g + m 4 g
FB = 5 m g
FB = 5 . 2 kg . 10 m/s²
|
|
No dejes de leer esta ADVRTENCIA de
No me salen |
|
|
|
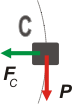 |
En la posición C no cabe duda que la velocidad es igual a la velocidad en A, ya que se encuentran a la misma altura. La ecuación de Newton para las fuerzas centrípetas, dirá:
ΣF = m acC
FC = m vC²/ L
|
|
|
|
FC = m vA²/ L
FC = m 2 g L / L
FC = m 2 g
|
|
|
|
|
|
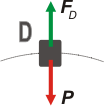 |
En la posición D la velocidad vale cero (dato del enunciado), de modo que se nos pone muy fácil.
ΣF = m aD
P — FD = 0
|
|
|
|
FD = m . g |
|
|
|
|
|
Ahora viene la última pregunta. ¿Todavía estas aquí? c- El contrapeso se lanza desde el punto A con
la misma velocidad que antes, pero ahora el rozamiento
en el eje hace que la varilla se detenga
en posición horizontal. Determinar el trabajo realizado
por las fuerzas de rozamiento en el recorrido
AC.
La nueva posición la voy a llamar C'. Entonces...
WFncAC' = EMC' — EMA
Acordate que pusimos el cero de las alturas en A.
WFncAC' = 0 — ½ m vA²
WFncAC' = — ½ m 2 g L
WFncAC' = — m g L
|
|
|
|
|
|
| |
|
|
 |
| DESAFIO: ¿Qué resultados habrían cambiado si el largo de la varilla fuera de 3,5 m? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-09. Buenos Aires, Argentina. |
|
|
|

