NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo, energía cinética, potencia, MCU)
|
|

|
| 2.2- Calcular el trabajo que realiza la fuerza
elástica en el resorte del problema 1.10 al comprimirlo
desde su posición original hasta la mitad
de ésta (Posición B). Comparar con la suma
de los trabajos calculados en dicho problema.
¿Es conservativa la fuerza elástica? ¿De qué modo
puede hallarse el trabajo de la fuerza elástica,
sin necesidad de evaluar el área bajo la gráfica
fuerza-elongación? |
|
| Supongamos que tenés presente al ejercicio 1.10 (en caso contrario andá y pegale un vistazo, yo te espero). En aquel caso hicimos el cálculo de los trabajos ( 0 → A y A → B) haciendo uso de la estrategia del cálculo de áreas en gráficos F-X; en este caso no están solicitando el trabajo 0 → B, y lo vamos a encarar por vía doble: cálculo de área y variación de energía potencial elástica. |
|
|
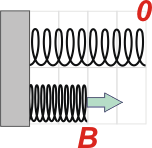 |
Empecemos con un esquema para que entres en órbita: Tenemos un resorte cuya longitud natural -sin estirar ni comprimir- es de 0,8 m (figura superior). Tomamos como referencia la posición de la espira extrema derecha (con perdón de la palabra), 0.
Se lo comprime hasta la mitad de su longitud, B. Y al estar comprimido (durante todo el trayecto) aparece la fuerza elástica, representada por una flecha verde.
El trabajo realizado por esa fuerza elástica es igual a menos la variación de energía potencial elástica. En símbolos: |
|
|
|
W0B = — (ΔEPe0B)
W0B = — (EPeB — EPe0)
W0B = EPe0 — EPeB
W0B = ½ k Δx0² — ½ k ΔxB²
La deformación en 0, Δx0, es nula, y el valor de la constante es 500 N/m (dato del ejercicio 1.10), de modo que la expresión se resume a:
W0B = — ½ 500 N/m . (0,4 m)²
|
|
|
|
|
|
Fijate que el enunciado del ejercicio pregunta sobre el trabajo de la fuerza elástica, o sea, el trabajo que realiza el elástico. Si preguntar por el trabajo que hace una fuerza externa para comprimir el elástico, el módulo del trabajo valdría lo mismo, ¡pero tendría signo opuesto!
Si lo resolvemos por la vía geométrica (integración de área)... |
|
|
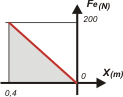 |
Para este ejercicio hubiera sido mejor utilizar un gráfico orientado al revés que éste, pero prioricé utilizar el mismo que el del ejercicio 1.10. Tené en cuenta que el desplazamiento es contrario al sentido de las equis (por lo tanto es negativo) y la fuerza elástica es contraria, positiva. (El ángulo que forma fuerza y desplazamiento es 180º). El área (se trata de un simple triángulo) representa el trabajo que estamos buscando. |
|
|
|
|
|  |
DESAFIO: Buscá dos o tres comprobaciones de que la fuerza elástica es conservativa.
|
|
| Algunos derechos reservados, y no los comparto con nadie, ¿entendiste?.
Se permite su reproducción citando la fuente. Última actualización jun-08. Buenos Aires, Argentina. |
|
|
|

