NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo, energía cinética, potencia, MCU)
|
|

|
 |
1.10- Se tiene un resorte cuya longitud sin carga
es 0,8 m, y su constante elástica es 500 N/m.
Dejando fijo un extremo, se lo estira hasta que su
longitud es el doble de la original (Posición A),
para luego comprimirlo hasta la mitad de su longitud
natural (Posición B).
Se pide: |
|
| a- |
Graficar la componente de la fuerza que
ejerce el resorte, en función de su elongación. |
| b- |
Determinar el trabajo que realiza la fuerza
elástica, al estirarlo desde la posición inicial hasta
A. |
| c- |
Hallar el trabajo realizado por la fuerza elástica
entre las posiciones A y B. |
|
| Hice un esquemita (no puedo evitarlo) para que veas cómo funciona el asunto. Ahí representé el mismo resorte en tres posiciones diferentes. La representación superior es la del resorte con su longitud natural, no está estirado ni comprimido. Así me lo vendieron en la ferretería. |
|
|
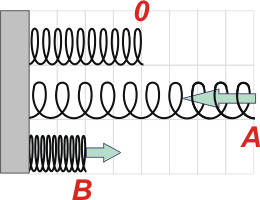 |
La posición de su extremo derecho nos va a indicar cuánto está estirado o comprimido. El otro extremo está sujeto a la pared. Dibujé una grilla en el fondo para que utilices como referencia.
Las flechas celestes representan a la fuerza elástica, Fe. Fijate que cuando el resorte fue estirado hasta la posición A, la fuerza del resorte tira para adentro. En cambio cuando el resorte fue comprimido hasta la posición B, la fuerza elástica empuja hacia afuera. |
|
|
|
| Por eso a las fuerzas elásticas se las llama restitutivas, porque siempre intentan recuperar la forma original. En el extremo pegado a la pared el resorte realiza una fuerza igual y contraria al extremo "libre". |
|
|
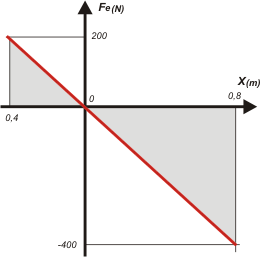 |
Acá tenemos el gráfico que representa la fuerza elástica en cualquier desplazamiento (entre B y A). Si referimos ambas variables (fuerza elástica y posición de la última espira) al mismo SR, entonces, cuando una es positiva, la otra negativa -chequealo-, así nos lo anticipaba la ley de Hoock:
Fe = — k x
Las áreas que sombreé en gris respresentan los trabajos que realiza la fuerza elástica durante los desplazamientos del extremo "libre". Para asignarle un signo a ese trabajo tenés que observar cuál es el sentido de la fuerza y cuál el sentido del desplazamiento. |
|
|
|
Luego: si el desplazamiento y la fuerza tienen igual sentido se trata de un trabajo positivo; y si fuerza elástica y desplazamiento tienen sentidos contrarios, estará realizando un trabajo negativo. Mientras el resorte se estira desde 0 hasta A, el estiramiento es positivo (tiene el mismo sentido de crecimiento que las posiciones) y la fuerza apunta en el sentido contrario, de modo que se trata de un trabajo negativo.
El viaje de A hasta B es más complicado, porque la fuerza elástica cambia de sentido en el medio. pero igual lo podés razonar. Y los trabajos son fáciles de calcular mediante las áreas, que también son sencillas ya que se trata de triángulos. El mayor vale 160 J y el menor 40 J (base por altura sobre dos). Con esos datos solos ya podrías resolver el ejercicio.
Pero también podés resolverlo analíticamente recordando que la energía elástica es igual a:
Ee = ½ k Δx²
Y para hallar la cantidad de trabajo que realiza la fuerza elástica entre dos posiciones cualesquiera basta con aplicar el teorema de las fuerzas conservativas, que dice que el trabajo de una fuerza conservativa es igual a menos la variación de la energía potencial generada por esa fuerza, en este caso, la energía potencial elástica, Ee:
W0A = — ΔEe0A
W0A = — ( EeA — Ee0 )
W0A = — ½ 500 N/m . 0,64 m² + 0
|
|
|
|
|
|
Lo mismo haremos para calcular el trabajo de la fuerza elástica entre A y B.
WAB = — ΔEeAB
WAB = — ( EeB — EeA )
WAB = — ½ 500 N/m . 0,16 m² + ½ 500 N/m . 0,64 m²
|
|
|
|
|
|
| |
|
 |
| DESAFIO: ¿Cuánto vale el trabajo de la fuerza que estira y/o comprime el resorte en este mismo ejercicio? |
|
| Algunos de mis derechos reservados, y no los comparto con nadie, ¿entendiste?.
Se permite su reproducción citando la fuente. Última actualización jul-08. Buenos Aires, Argentina. |
|
|
|

