NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo, energía cinética)
|
|

|
 |
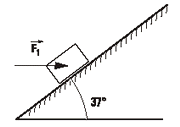
1.7 El bloque de 50 kg asciende por el plano inclinado
de la figura y recorre 2 m sobre el mismo,
con la fuerza horizontal constante F1 aplicada,
de 600 N. También actúa una fuerza de rozamiento
de 100 N.
Hallar: |
 |
|
a- El trabajo que realiza F1
b- El que realiza la fuerza de rozamiento.
c- El que realiza el peso del bloque.
d- El que realiza la fuerza de vínculo, normal
al plano.
e- La fuerza resultante que actúa sobre el bloque,
y su trabajo.
f- La velocidad del bloque luego de ascender
los 2 m, si al comienzo tenía una velocidad de
0,6 m/s.
g- Las energías cinéticas inicial y final del bloque.
Qué puedo decirte... laaaargo como esperanza de pobre. Pero creo que es un problema bastante aleccionador. Vamos a hacerlo y armate de paciencia.
Hagamos un DCL para visualizar todas las fuerzas que están actuando y sus direcciones relativas con el desplazamiento. |
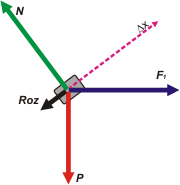 |
Ahí están, son 4 fuerzas: F1, P, Roz y N. Y en punteado representé el desplazamiento (los largos de las fuerzas son aproximadamente representativos entre sí, y el del desplazamiento tiene un largo arbitrario, ya que es una magnitud diferente).
Vamos a calcular el trabajo que hace cada una de las fuerzas a lo largo de ese desplazamiento. Usaremos siempre
W = F . Δx . cos α
donde α es el ángulo que en cada caso, formen el desplazamiento con la fuerza en cuestión. |
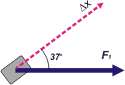 |
| Empecemos con F1 |
WF1= F1 . Δx . cos 37º
|
WF1= 600 N . 2 m . 0,8
|
| a) |
WF1= 960 J |
|
|
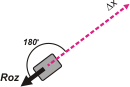 |
| Seguimos con Roz |
WRoz = Roz . Δx cos 180º
|
WRoz = 100 N . 2 m . (-1)
|
| b) |
WRoz = — 200 J |
|
|
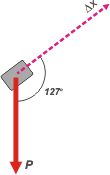 |
| Ahora le toca al peso. No siempre se distingue claramente cuál es el ángulo que forman entre la fuerza y el desplazamiento. Arreglátelas como puedas. Acá, por ejemplo no es muy difícil verlo como la suma de 37 más 90, o sea 127 grados. |
WP = P . Δx . cos 127º
|
WP = 500 N . 2 m . (-0,6)
|
| c) |
WP = — 600 J |
|
|
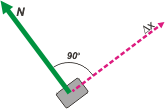 |
| El turno de la fuerza de apoyo, N |
WN = N . Δx . cos 90º
|
WN = N . 2 m . 0
|
| d) |
WN = 0 J |
|
|
| Y ahora le toca el turno a la resultante de las cuatro fuerzas. Pero no sabemos cuánto vale ni hacia dónde apunta (sospecho que debe ser paralela al plano... ¿vos no tenés la misma sospecha?, bueno... mejor tenela) Descompongamos en x y en y, y sumemos por separado. |
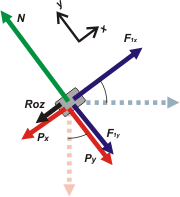 |
En x
Resx = F1x — Roz — Px
Resx = F1 cos 37º — Roz — P sen 37º
Resx = 600 N 0,8 — 100 N — 500 N 0,6
Resx = 80 N
En y
Resy = N — F1y— Py = 0
|
| Si la resultante en y no fuese cero, el bloque levantaría vuelo o se hundiría en el plano, por eso, aunque no sabemos cuánto vale N, sabemos cuánto vale esa suma. Luego, si componemos la resultante obtenemos Res = 80 N paralela al plano y hacia arriba. |
 |
| Su trabajo en el desplazamiento será |
WRes = Res . Δx . cos 0º
|
WRes = 80 N . 2 m . 1
|
| e) |
WRes = 160 J |
|
|
|
|
| No te olvides que en la definición de trabajo hay que usar el módulo de F y el módulo de Δx; el signo de un trabajo está dado por el coseno del ángulo qe forman F con Δx. |
|
| Paremos la pelota un cachito. Dejame que resuma, a ver... |
|
WF1 = 960 J |
|
+ |
WRoz = — 200 J |
+ |
| |
WP = — 600 J |
|
| |
WN = 0 J |
|
| e) |
WRes = 160 J |
|
|
|
|
|
No se trata de una casualidad de este problema. Siempre ocurre que la suma de todos los trabajos de todas las fuerzas que actúan sobre un cuerpo, es igual al trabajo de la resultante. Si lo querés en una fórmula...
WRes = ΣWFi
Bueno, ahora vamos a las últimas preguntas. Vamos a resolverlo por cinemática, ya que, por Newton, si tenemos la resultante también tenemos la aceleración.
|
|
|
| a = |
Res |
= |
80 N |
= 1,6 m/s² |
|
|
|
| m |
50 kg |
|
|
|
Llamemos 0 y F a los puntos inicial y final del trayecto de los 2 metros. Luego de las ecuaciones correspondientes y tomando to y xo igual a cero...
x = 0,6 m/s t + 0,8 m/s² . t2
v = 0,6 m/s + 1,6 m/s² t
le pedimos que hablen de punto F
2 m = 0,6 m/s tF + 0,8 m/s² . tF2
vF = 0,6 m/s + 1,6 m/s² tF
Dos ecuaciones con dos incógnitas. De la primera sacamos tF... eso da... a ver... uso la cuadrática de los griegos, mmm... tF = 1,25 s Con esto voy a la segunda ecuación y obtengo... |
|
|
|
|
|
Pero ahora también podemos resolver el problema de un modo más sencillo, fijate, respondamos la última pregunta que nos queda
EC0 = ½ m v0² y ECF = ½ m vF²
|
|
|
| g) |
EC0 = 9 J y ECF = 169 J |
|
|
|
|
| Con lo cual se ve claramente que
WRes = ΔEC
Y acá teníamos el otro camino, mucho más sencillo con este teorema que relaciona el trabajo de la resultante con la energía cinética.
WRes = ECF — EC0
WRes = ½ m vF² — ½ m v0²
vF² = (2 WRes /m) + v0²
vF² = (2 . 160 J /50 kg ) + 0,36 m²/s²
vF = 2,6 m/s
|
|
¿Tenés ganas de leer algo que te rompa la cabeza? |
| |
| |
| DISCUSION: La principal lección de este ejercicio es la diferencia de estrategia en la resolución de un mismo problema. El uso del criterio de trabajo y energía es más económico, más directo, consiste en comparar directamente dos estados de un proceso desinteresándonos de cómo fue el proceso. Hay mucha información que se pierde, pero se gana en economía. También hay una nueva información que aparece, y que es la energía... pero cuyo significado debe madurar largamente, pues no hay una explicación concreta para ella. |
|
 |
| DESAFIO: ¿Cuánto vale la fuerza de vínculo? (ese es muy pavo). (Pero este otro...) ¿a qué altura la velocidad del cuerpo será 5 m/s? |
|
| Agradezco la lectura atenta de Federico Muller, que detectó una errata y me lo avisó en un gentil e-mail. Todos los derechos reservados, incluido el derecho de asesinar de 20 cuchilladas, dos balazos y envenenamiento con una mezcla 30:70 de cianuro y estricnina a quien osare reproducir este material sin mencionar a su autor, que es un santo incapaz de pisar una hormiga. Última actualización jul-07. Buenos Aires, Argentina. |
|
|
|

