NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(conservation laws, work)
|
|

|
 |
1.4- Claudia weighs 60 kgf, and goes down in an elevator from the 4th floor to ground floor. Find the work done by the force that makes the floor of the elevator («normal») on her, in the following segments of 4 meters lenght each:
a- Constant starting acceleration of 0,5 m/s²
b- Constant descending speed of 2 m/s
c- Constant braking acceleration of 0,5 m/s². |
|
|
The endless problem of the elevator (I was going to say -men-) which is showed now in a work definition version. Well, the trip is divided into three different dynamics sections, which we call a), b) and c) and they represent a common trip going down from the 4th floor to the ground floor.
Three cases. In these three cases there are only two forces acting on Claudia: her weight, P, it means the force with which the Earth has her trapped, and the normal, N, the force with which the floor of the elevator holds her, and it's called normal because it has 90 degrees from the floor. If that force wouldn't exist, Claudia would fall through the shaft, and it would be a shame... so young, so pretty...
The three cases are, dinamically, very similar. Newton's equation will say:
ΣF = m a
It is enough with only one equation beacuse each forces are vertical. And if i choose a Reference System positive pointing up, the equation will be:
N — P = m a
Acceleration varies in all three cases (and this modifies the second segment). Then, from the first segment we can only modify the normal force, since Claudia weight may not vary much during her travel from the 4th floor to the ground . Once we know its value, we can calculate its work in 4 meters of descent. |
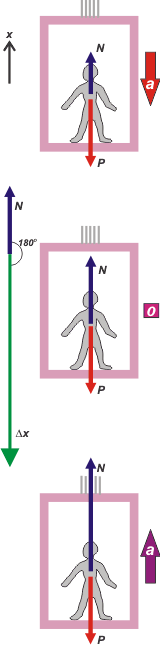 |
a) If it starts and moves faster all the time, acceleration must be pointed down. (In our Reference System it will be negative, a = — 0,5 m/s²)
N = m a + P
N = 60 kg . (—0,5 m/s²) + 600 N
N = — 30 N + 600 N
N = 570 N
Wa) = 570 N . 4 m (—1)
|
|
b) when it goes down with constant speed, if it is done by 2 m/s or 200 m/s is the same according to what we're calculating. That information is just a fools trap. Acceleration is zero.
N = P
N = 600 N
Wb) = 600 N . 4 m (—1)
|
|
c) When it goes down braking, acceleration points up and in our Reference System is possitive.
N = m a + P
N = 630 N
Wc) = 630 N . 4 m (—1)
|
|
|
|
|
Check the "work" definition (we could aplly it here because our force is constant, and the displacement is straight for each section) it doesn't depend on the RS. The sign (possitive or negative) of the work depends on the cosine of the angle formed by the force and displacement. And nothing else. In this case, displacement goes always down and the force that the floor is making always points up. So this always makes a 180 degrees angle, and cosine(180º) = (—1). |
|
|
| |
| |
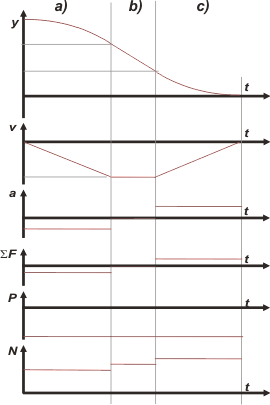
| DEBATE: I don't know if you ever seen this before, but I think this is an excellent way to talk it over. Draw everything you can draw to describe the problem. Here i give you some, take a look at them carefully, and check how are they related between them, I kept some proportionalities and I made them match according to their segments... but do not think that all possibilities are exhausted just with this, huh? you can still add two or three more graphics. |
 |
|
|
 |
| CHALLENGE: Remake the graphics, but hand-made, for a similar trip but in this case starting from the ground till the 4th floor.. |
|
| Translated by Matías Llofriú. Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|