NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo)
|
|

|
 |
1.4- Claudia pesa 60 kgf, y viaja en un ascensor
desde el piso 4° hasta planta baja. Hallar el trabajo
que realiza la fuerza que hace el piso del ascensor
(«normal») sobre ella, en los siguientes
tramos de 4 m de longitud cada uno:
a- Arranque con aceleración constante, de
0,5 m/s²
b- Descenso con velocidad constante de 2 m/s
c- Frenado con aceleración constante, de
0,5 m/s². |
|
El eterno problema del ascensor (iba a decir de los hombres) que ahora aparece en una versión de definición de trabajo. Bueno, el viaje lo dividimos en tres tramos de dinámica diferente, que llamaremos a), b) y c) y que representan un viaje común y silvestre en ascensor bajando del 4to piso hasta la planta baja.
Los tres casos. En los tres casos hay sólo dos fuerzas actuando sobre Claudia: su peso, P, o sea la fuerza con que la Tierra la tiene atrapada, y la normal, N, la fuerza con que la sostiene el piso del ascensor, que se llama normal porque forma 90 grados con el piso. Si esa fuerza no estuviera, Claudia caería por el hueco del ascensor, y sería una pena... tan joven, tan bonita...
Los tres casos, entonces, son muy parecidos dinámicamente. Para los tres, la ecuación de Newton dirá:
ΣF = m a
Alcanza con una sola ecuación pues ambas fuerzas son verticales. Y si elijo un SR positivo hacia arriba la ecuación queda así:
N — P = m a
En cada uno de los tres casos varía la aceleración (y eso modifica el segundo miembro) Luego, del primer miembro sólo puede modificarse la normal ya que el peso de Claudia no puede variar mucho en el transcurso de su viaje del 4to a la planta baja. Una vez que sabemos cuánto vale, podemos calcular su trabajo en 4 m de descenso. No te olvides de que 60 kgf son 600 N. |
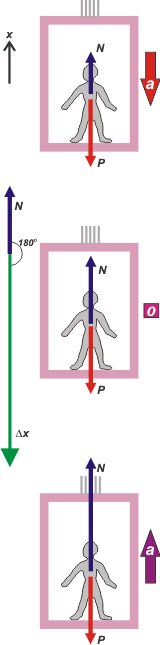 |
Caso a) Si arranca y se mueve caca vez más rápido la aceleración debe apuntar hacia abajo. (En nuestro SR serás negativa, a = — 0,5 m/s²)
N = m a + P
N = 60 kg . (—0,5 m/s²) + 600 N
N = — 30 N + 600 N
N = 570 N
Ahora el trabajo:
Wa) = 570 N . 4 m (—1)
|
|
Caso b) cuando baja a velocidad constante, si lo hace a 2 m/s o a 200 m/s es lo mismo a los fines de lo que estamos calculando. El dato ese es simplemente una trampa caza-bobos. La aceleración vale cero.
N = P
N = 600 N
Wb) = 600 N . 4 m (—1)
|
|
Caso c) Cuando baja frenando la aceleración apunta hacia arriba y en nuestro SR es positiva.
N = m a + P
N = 630 N
Wc) = 630 N . 4 m (—1)
|
|
|
|
|
Fijate que la definición de trabajo (que acá pudimos aplicar porque en cada tramo la fuerza es constante y el desplazamiento rectilíneo) es independiente del SR. El signo del trabajo depende exclusivamente del coseno del ángulo que forman la fuerza y el desplazamiento. De nada más que eso. En este caso el desplazamiento siempre es hacia abajo y la fuerza que hace el piso siempre apunta hacia arriba. De modo que siempre forman un ángulo de 180 grados y el coseno de 180º es (—1). |
|
|
| |
| |
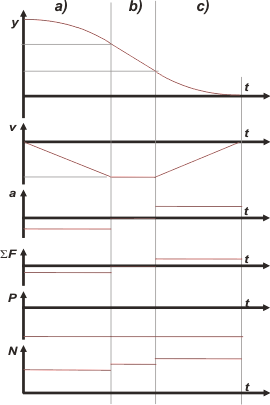
DISCUSION: No sé si alguna vez lo viste, pero me parece una excelente manera de discutir un problema hacer todos los gráficos posibles que lo describen.
Acá te pongo algunos, analizalos con cuidado, fijate cómo se relacionan unos con otros, mantuve ciertas proporcionalidades, y correspondencia entre intervalos... pero no creas que con éstos se agotan las posibilidades, ¿eh?, todavía vas a poder agregarle dos o tres gráficos más.
Están representados los tres movimientos uno a continuación de otro. Se trata de una situación típica de una ascensor que baja desde el cuarto piso a la planta baja.
|
 |
|
|
 |
| DESAFIO: Rehacer los gráficos, a mano alzada, para un viaje similar a éste pero de planta baja hasta el cuarto piso. |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco la atenta lectura de Emiliano Romanelli, que detectó un error de tipografía y me envió la corrección. Última actualización dic-06. Buenos Aires, Argentina. |
|
|
|

