 |
NO ME SALEN
EJERCICIOS RESUELTOS DE BIOFÍSICA DEL CBC
(Leyes de conservación, trabajo) |
|
|

|
| |
 |
EM22) Sobre un cuerpo que se desplazó 2 m por un camino horizontal actuó una fuerza, F. El
trabajo realizado por dicha fuerza fue de 150 J. ¿Cuál de los siguientes gráficos representa
la componente horizontal de la fuerza F en función de la coordenada de posición horizontal
x? |
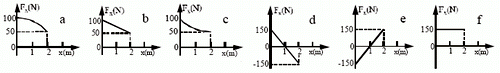 |
|
|
Ya sé que se ven mal, no te preocupes... abajo los amplío y los analizamos con detalle. Mirá, este ejercicio es muy sencillo... pero es importantísimo. Todo consiste en utilizar la siguiente propiedad:
en todo gráfico de fuerza en función de la posición, el área encerrada bajo la curva en un desplazamiento cualquiera representa el trabajo de dicha fuerza en ese desplazamiento.
Y no importa qué tipo de función sigue la fuerza: si es constante, si varía linealmente, si cambia de signo. Las cuestiones que requieren cierto cuidado son: debe tratarse de una fuerza paralela al desplazamiento (eso ocurre en nuestro ejercicio); las áreas sobre el eje de posición representa trabajos positivos, y debajo del eje, trabajos negativos. Puse un poquito más de información en este otro ejercicio que -además- te recomiendo.
Analicemos uno por uno, y dejame elegir el orden a mí, así lo uso para ir enseñándote los trucos del oficio. Vamos con el f que es el más sencillo: |
|
|
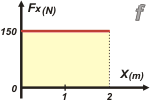 |
Como ves, el área encerrada bajo la curva es un simple cuadrilátero rectángulo. Para hallar la superficie de un rectángulo multiplicábamos base por altura... de modo que el trabajo en el desplazamiento de los dos metros es
Wf = 150 N . 2 m
|
|
|
|
|
Queda claro que no era ése el nuestro. Vamos al e. |
|
|
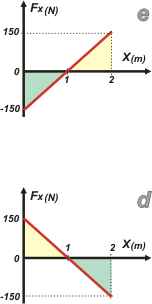 |
Ahora quedaron definidas dos áreas: una debajo del eje x, que pinté de verde, y otra arriba, que pinté de amarllo. Cada uno es un triángulo cuyo área se obtiene multiplicando la base por la altura y dividiéndolo por dos, y representan: el trabajo de la fuerza desde la posición 0 hasta 1 metro, We0-1, y el trabajo de la fuerza desde la posición 1 hasta 2 metros, We1-2.
We0-1 = — 150 N . 1 m . ½ = — 75 J
We1-2 = 150 N . 1 m . ½ = 75 J
Y el trabajo desde la posición 0 hasta 2 metros será la suma de los dos trabajos parciales recién calculados:
We = We0-1 + We1-2
Con el gráfico d pasa exactamente lo mismo que con éste. No cambia en nada el hecho de que en el e la fuerza sea linealmente creciente respecto de la posición y en el d sea decreciente. Lo que importa es que las áreas a distintos lados del eje x representan trabajos de distinto signo, que se cancelan entre sí, en ambos casos totalmente. |
|
|
|
|
| Vamos al b, que, además de fácil, es el que pide el enunciado. |
|
|
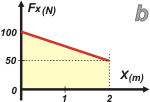 |
El área encerrada bajo la curva (curva es un término que en nuestra jerga adquiere carácter genérico, es aplicable a una recta, como en este caso) vale 150 J. Podés calcularlo como la suma de un rectángulo más un triángulo. O, si no, base por altura media.
Wd = 2 m . ½ (100 N + 50 N)
|
|
|
|
|
| Y dejamos para el final los más interesantes, el a y el c. |
|
|
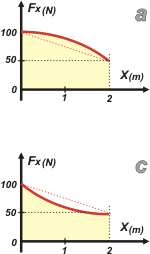 |
No importa cuál es la función, F(x), ni qué forma tienen las gráficas, serán parábolas, serán elipses, serán elipses hiperbólicas ortogonales... realmente no importa. Lo que sí importa es que estimes correctamente el área que cada una encierra bajo la curva. Si las comparás con un área de referencia (justo el área que calculamos para el gráfico anterior, que era un trapecio) podés deducir correctamente que ambas son diferentes de 150 J, que es lo único que nos interesa.
Para ayudarte a hacer la comparación tracé, en cada uno, una recta oblicua (punteada roja) que coincide con la función b, y que delimita el área del trapecio que calculamos antes. Ahora es fácil: |
|
| |
|
|
|
|
| |
|
|
DESAFIO: En los gráficos d y e aparece un conflicto físico muy, pero muy, interesante. No pretendo que lo resuelvas... porque no es nada sencillo. Pero sí pretendo que lo descubras. ¿Te animás? |
|
 |
| |
|
| |
|
| Algunos derechos reservados.
A vos... y sólo a vos... te permito copiar este material por cualquier medio, gráfico o electrónico, y regalárselo a tu sobrino, o venderlo, o tirarlo, o hacer con él lo que quieras. Última actualización sep-08. Buenos Aires, Argentina. |
|
|
|

