NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de conservación, trabajo)
|
|

|
 |
1.9- El gráfico de la figura representa la componente
Fx de una fuerza que actúa sobre un
cuerpo que se mueve sobre una recta paralela al
eje x, en función de su posición.
|
|
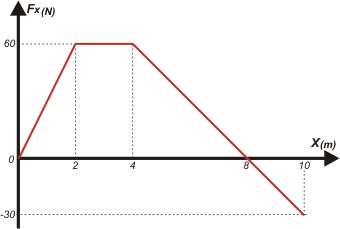
Calcular el trabajo que realiza dicha fuerza, en
las siguientes etapas:
a- Desde la posición x1= 0 hasta x2= 4 m.
b- Entre x2 y x3= 10 m.
c- Entre x1 y x3. |
Este problema es muy sencillo, se trata simplemente de calcular áreas. Resulta (y esto te lo cuento sólo por agregar algo que pueda interesarte) que la definición extensa de trabajo requiere el concepto de integral.
W = ∫ Fx dx
que, si hacés un poco de memoria, se relaciona con el cálculo de áreas encerradas bajo la curva (en este caso la curva de F vs. x). Efectivamente, si vos hallás el área encerrada bajo la curva en cualquier gráfico F vs. x, tenga la forma que tenga, lo que estás haciendo no es un cálculo de superficie meramente sino un cálculo de trabajo.
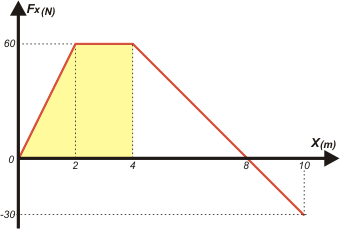
El ítem a) pide calcular este trabajo, el representado por este área: |
|
|
 |
|
|
| Te la sombreé en amarillo para que la distingas bien. En definitiva es una figura geométrica bien sencilla, un trapecio. Pero si no te acordás cómo se hallaba el área de un trapecio podés encontrarla como la suma del área de un triángulo (base por altura sobre dos) más el área de un rectángulo (lado por lado). El triángulo da 60 y el rectángulo 120. Fijate las unidades... |
|
|
|
|
|
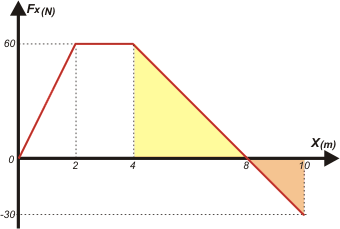
| El ítem b) pide el trabajo entre 4 y 10 metros. Acá tenés ese área: |
|
|
 |
|
|
| La pinté en dos colores diferentes porque tiene significado físico. El área que queda por debajo del eje de las x representa un trabajo negativo. Lo cual es lógico ya que el desplazamiento y la fuerza, al tener signo contrario, formarían un ángulo de 180 grados, y su coseno valdría -1. Calculamos ambas áreas y las sumamos, cada una con su signo. |
|
|
|
|
|
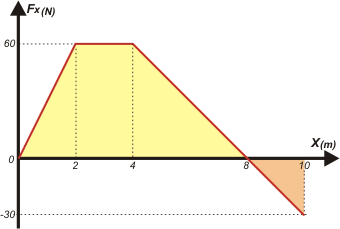
| Por último, el ítem c) pide el trabajo entero. Como siempre el trabajo total es la suma de los trabajos parciales (siempre y cuando no se superpongan). Igual te hice el gráfico. |
|
|
 |
|
|
|
| |
Ya en cinemática podíamos hacer algunos cálculos integrando áreas, ¿te acordás? En toda gráfica v vs. t el área encerrada bajo la curva representaba el desplazamiento del móvil en el intervalo de tiempo encerrado. Es exactamente la misma idea que ahora, solo que entonces era:
ΔX = ∫ v dt
y nadie salió lastimado. |
|
 |
| DESAFIO: si la operación inversa de la integración es la derivación, ¿te animás a formular relaciones entre magnitudes físicas en términos de funciones derivadas? |
|
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. A quien violase esta cláusula se lo enclaustrará por violador de cláusulas. Última actualización nov-06. Buenos Aires, Argentina. |
|
|
|

