 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA DEL CBC
(Leyes de conservación)
|
|

|
CHOQUES
Los conceptos de impulso y cantidad de movimiento permiten encontrar una ley de conservación muy útil e interesante. Miremos lo que pasa en un choque.
|
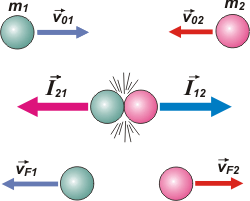 |
Acá tenemos un modelo de choque. Dos cuerpos de masas m1 y m2 se mueven con velocidades de encuentro, v01 y v02.
En determinado instante chocan. El contacto es muy breve, pero no instantáneo. Dura un cierto intervalo de tiempo, Δt. Multiplicando ese intervalo por la fuerza que cada uno le hace al otro (un par de interacción), podemos definir el impulso que el cuerpo 1 le hace al 2, I12; y un impulso que el 2 le hace al 1, I21. |
|
|
|
Al igual que las fuerzas de interacción, los impulsos entre ambos son iguales en módulo, iguales en dirección y de sentido contrario.
I21 = — I12
El impulso que recibe cada cuerpo es igual a la variación de su cantidad de movimiento.
Δp1 = — Δp2
m1 vF1 — m1 v01 = — (m2 vF2 — m2 v02)
Podemos reordenar los términos juntando en un miembro lo que tiene que ver con el momento anterior al choque y en el otro miembro lo de después.
m1 v01 + m2 v02 = m1 vF1 + m2 vF2
p01 + p02 = pF1 + pF2
Y mirá lo que pasa si definimos cantidad de movimiento total, como la suma de las cantidades de movimiento de ambos cuerpos:
p0T = pFT
Dicho de otro modo: |
|
|
| |
|
|
En un choque la cantidad de movimiento total del sistema no varía. La cantidad de movimiento total del sistema es una magnitud que se conserva.
La ecuación más práctica en la resolución de problemas de choque es ésta: |
|
|
| |
m1 v01 + m2 v02 = m1 vF1 + m2 vF2 |
para todos los choques |
|
|
|
| No es infrecuente que los cuerpos queden unidos después de chocar. A ese tipo de choques se los llama choques plásticos, y se describen con la misma ecuación, pero ya que las velocidades finales de ambos cuerpos son iguales (ya que quedaron unidos) se puede tomar esa velocidad final como factor común: |
|
|
| |
m1 v01 + m2 v02 = ( m1 + m2 ) vF |
para los choques plásticos |
|
|
|
El principal recaudo que hay que tomar para usar estas ecuaciones es recordar el carácter vectorial de las velocidades: no hay que olvidarse de establecer un Sistema de referencia y asignarle signo a cada velocidad antes de operar algebraicamente.
Si los cuerpos chocan con velocidades de direcciones diversas (no unidireccionales) habrá que hacer un planteo para cada dirección del SR, descomponiendo aquellas que no coinciden con ellas. Por ejemplo, en un choque bi-dimensional habrá que plantear dos ecuaciones: |
|
|
| |
m1 v01x + m2 v02x = m1 vF1x + m2 vF2x
m1 v01y + m2 v02y = m1 vF1y + m2 vF2y |
para todos los choques
bi-dimensionales |
|
|
|
CHISMES IMPORTANTES: |
|
|
- Lo que encontramos aquí para un choque entre dos cuerpos se puede extender a un sistema de muchos cuerpos. Y también se puede extender a cualquier tipo de interacciones (no necesariamente de contacto). Lo puedo resumir así: en un sistema aislado la cantidad de movimiento total se conserva. Acá una pequeña listita de sistemas donde podríamos aplicar esa Ley: una explosión, un choque múltiple, una galaxia en movimiento, un sistema planetario...
|
|
|
PREGUNTAS CAPCIOSAS: |
|
|
- ¿Te animarías -al menos en palabras- a definir le ley de conservación de cantidad de movimiento angular?
|
|


|
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Última actualización jun-09. Buenos Aires, Argentina. |
|
|
|

