 |
NO ME SALEN
APUNTES TEORICOS DE FÍSICA DEL CBC
(Leyes de conservación)
|
|

|
TIPOS DE CHOQUES
(Conservación de la energía durante un choque)
Salvo raras excepciones, durante un choque se pierde energía. La energía perdida va a parar a otras formas de energía (el principio general de conservación de la energía sigue valiendo) que salen del sistema y en general se transforman en energías inservibles, inaprovechables. Por ejemplo: deformación de los cuerpos, calor, ruido...
La pregunta cuánta energía se perdió es pertinente y vale la pena formularla. Como los choques suelen ocurrir localizados en una posición, no solemos evaluar la energía potencial (suponemos que no va a variar), y nos concentramos en la energía cinética. |
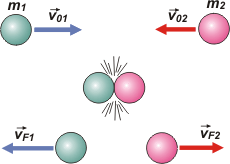 |
La energía antes de chocar es:
E0 = ½ m1 v01² + ½ m2 v02²
Y después de chocar:
EF = ½ m1 vF1² + ½ m2 vF2²
La variación es lo que nos interesa:
ΔE = EF – E0 |
|
|
|
|
|
|
La pérdida de energía suele ser mayor en los choques plásticos, ya que parte de la energía hay que invertirla en unir los cuerpos. La pérdida de energía puede llegar a ser total; en ese caso la energía final valdrá cero. |
|
|
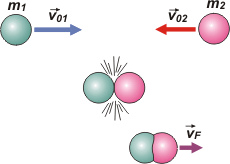 |
No hay modo de predecir qué porcentaje de energía se va a perder durante el choque, pero suele ser importante.
Las explosiones se abordan exactamente igual que los choques plásticos. Antes de la explosión los fragmentos (futuros fragmentos) están todos unidos; después de la explosión cada fragmento vuela por su cuenta... pero la suma de sus cantidades de movimiento es igual a la cantidad de movimiento que tenía la bomba intacta antes de explotar (habitualmente cero). |
|
|
|
En la situación opuesta podemos tener choques en los que no se pierda nada de energía. Este tipo de choques se denominan perfectamente elásticos. (Se trata, habitualmente de situaciones ideales, no reales). Para tener choques en los que no se pierda nada de energía los cuerpos que chocan deben ser perfectamente elásticos o chocar teniendo en medio un elástico perfecto e ideal.
El choque perfectamente elástico estará representado por esta ecuación:
½ m1 v01² + ½ m2 v02² = ½ m1 vF1² + ½ m2 vF2²
que nos dice que la energía antes del choque es la misma que la de después del choque. |
|
|
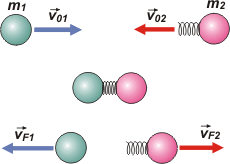 |
Este es un modo típico de simbolizar un choque perfectamente elástico. Aunque no es necesaria la interposición del resorte: alcanza con que nos digan que los cuerpos son suficientemente elásticos, o -mejor aún- que el choque es perfectamente elástico.
Si se da le caso, no vale la pena mantener el factor común (½). Un choque así queda descripto por las dos ecuaciones: la de conservación de la cantidad de movimiento y la de conservación de la energía:
|
|
|
|
| Las dos ecuaciones son muy parecidas... pero es sólo apariencia: ¡son totalmente diferentes! |
|
|
| |
m1 v01 + m2 v02 = m1 vF1 + m2 vF2
m1 v01² + m2 v02² = m1 vF1² + m2 vF2² |
para los choques
perfectamente elásticos |
|
|
|
Cambios de energía individuales. Otra pregunta interesante (y pertinente) es ¿cuánta energía perdió o ganó un cuerpo durante un choque? Efectivamente... se trate del tipo de choque que se trate, cualquiera de los cuerpos que intervienen en un choque puede ganar o perder energía. No importa si esta libre o unido, para conocer el cambio de energía de un cuerpo i de masa mi, procedemos así:
ΔEi = EFi – E0i
ΔEi = ½ mi vFi² – ½ mi v0i²
Y basta. Me cansé. |
|
|
CHISMES IMPORTANTES: |
|
|
- Supongamos que el universo se comportara de esta manera: que la energía no fuese una magnitud continua sino que sus intercambios fueran de a paquetes, cantidades mínimas que no se pudiesen fraccionar. (Esta suposición es tan ridícula que hasta me da vergüenza plantearla). Llamemos cuanto a esa cantidades mínimas de energía. Si un choque entre dos corpúsculos fuera tal que la pérdida de energía fuese menor que un cuanto, entonces, no puede perderla, y el choque se convierte en perfectamente elástico. Cosas de la cuántica.
|
|
|
PREGUNTAS CAPCIOSAS: |
|
|
- ¿Por qué a las explosiones los físicos a veces las llaman choque explosivo?
- En una explosión, la energía cinética de los fragmentos después de explotar resulta siempre enormemente superior a su energía cinética antes de explotar (relativamente: cero). ¿De dónde salió esa energía?
|
|
 |
| |
| Algunos derechos reservados.
Se permite su reproducción citando la fuente. Agradezco a Guillermo Anglada por el envío de una errata. Última actualización jul-09. Buenos Aires, Argentina. |
|
|
|

