TRABAJO de la FUERZA PESO

La fuerza peso (el nombre vulgar que le damos a la fuerza gravitatoria cuando se ejerce cerca de la superficie de la Tierra) es el arquetipo de las fuerzas conservativas, aquellas en las que el trabajo no depende de la trayectoria sino de las posiciones inicial y final exclusivamente.

Vamos a calcular su trabajo cuando se está aplicada sobre un cuerpo que se desplaza desde el punto A hasta el punto B (dos posiciones cualesquiera del espacio).

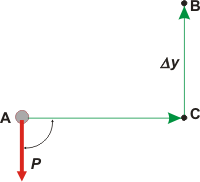
Vamos a hacer el cálculo para varios caminos diferentes. Primero por este camino que llamaremos 1 (¹W_P).

Si a la diferencia de alturas entre C y B la llamos Δy, nos queda:

¹W_P = 0 + P Δy cos 180°

¹W_P = — m g Δy

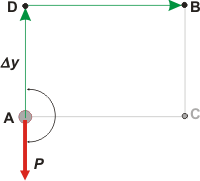
Ahora probemos por un camino alternativo: nuevamente trayectorias rectas, esta vez pasando por el punto D, que se halla en la misma vertical que A y al mismo nivel que B. A este camino lo llamaremos 2, y , nuevamente, particionamos:

Por lo tanto:

²W_P = — m g Δy

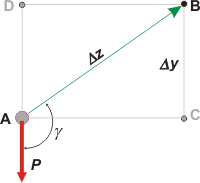
El mismo resultado que por el camino 1. Probemos ahora por el camino más corto y directo entre A y B, o sea por la recta que los une. A este camino lo llamaremos 3, y al segmento AB, Δz.

Entonces:

³W_P = — P Δz sen α

Pero Δz sen α es igual a Δy. Con lo que llegamos al mismo resultado que en los caminos anteriores.

³W_P = — m g Δy

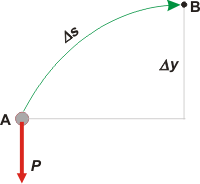
Todo esto no quiere decir mucho, ya que los tres caminos elegidos hasta ahora son bastante particulares y arbitrarios. Probemos por un camino totalmente diferente, una curva cualquiera que una A con B. A este camino lo llamaremos 4.

        ⁴W_P = ^4,1W_P + ^4,2W_P + ^4,3W_P + ... + ^4,nW_P

        ⁴W_P = P Δs₁ cos γ₁ + P Δs₂ cos γ₂ + P Δs₃ cos γ₃ + ... + P Δs_n cos γ_n

Cada uno de esos segmentos es equivalente al caso del camino 3, o sea, sin importar cuánto valga α_i el resultado va a ser el mismo: P Δs_i cos α_i = — P Δy_i

 ⁴W_P = — P Δy₁ — P Δy₂ — P Δy₃ — ... — P Δy_n

Sacamos factor común P en todos esos términos...

⁴W_P = — P (Δy₁ + Δy₂ + Δy₃ + ... + Δy_n)

Y la suma de todas las pequeñas diferencias de altura de cada porción de desplazamiento no es otra cosa la la diferencia de altura total entre A y B, o sea, Δy.

⁴W_P = — m g Δy

Como este no fue un camino en particular si no uno cualquiera, entonces ahora sí podemos generalizar y decir que el trabajo de la fuerza peso entre un par de posiciones cualesquiera vale siempre lo mismo independientemente de cuál haya sido la trayectoria entre esas dos posiciones.

Si recordamos que Δy = (y_B — y_A), y llamamos energía potencial gravitatoria en A, E_PA, al producto m g y_A; y lo mismo para B, y nos queda:

CHISMES IMPORTANTES:

• Si te parece medio trucho transformar una curva en una sucesión de segmentos rectos, podés imaginar segmentos mucho más chiquitos. Y así... te corro. El análisis matemático te demuestra que el error que cometés al tomar segmentos impensablemente cortos es nulo.
• Escribir m g y_B o m g h_B es lo mismo. Pero recordá que las alturas se definen siempre de esta manera: lo que está más arriba tiene un número mayor. O sea: el Sistema de Referencia de alturas debe apuntar hacia arriba, no importa dónde coloques el cero.

PREGUNTAS CAPCIOSAS:

• Si la energía potencial gravitatoria de cualquier cuerpo depende del Sistema de Referencia que elija, o sea, de dónde se coloca el cero de las alturas, ¿por qué eso no afecta a las Leyes de conservación ni a los teoremas de trabajo?
• Cuanto valdrá el trabajo de la fuerza peso sobre una avioneta de 600 kg. que sale volando de un aeródromo realiza tres vuelos verticales, 8 loops, 6 caídas libres, 2 tirabuzones, 5 zig-zags y regresa al mismo aeródromo del que partió?