 |
NO ME SALEN
PROBLEMAS RESUELTOS DE FÍSICA DEL CBC
(Leyes de Newton)
|
|

|
No me salen d5.02* - Una masa cuelga en reposo del techo
de un coche de ferrocarril detenido en una vía
horizontal mediante un resorte de constante k. El tren arranca con aceleración
constante, y como consecuencia de ello, el resorte se inclina se estira. Expresar el ángulo de inclinación con la vertical y el estiramiento del resorte en función de la aceleración del vagón y de la masa.
Este es un problema muy bonito, descendiente directo por parte de madre del d1.11, que espero que ya hayas resuelto. Voy a hacer dos DCL, el de la izquierda cuando el tren está en reposo y el de la derecha cuando todo el conjunto acelera. |
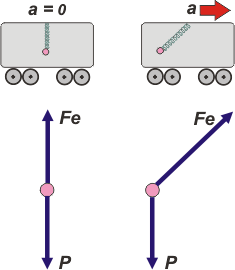 |
Indudablemente el que nos interesa es el segundo DCL, aquél que representa las fuerzas que obran sobre el péndulo cuando el vagón está acelerado. Observá que no han aparecido nuevas fuerzas. Las únicas dos que actúan son: P, la fuerza con que la Tierra solicita al péndulo, y Fe, la fuerza que ejerce la cuerda que, por supuesto debe tener la misma dirección que la cuerda.
De ése DCL va a salir la solución del problema. Por un lado sabemos que para un resorte de constante k, la fuerza elástica que produce es proporcional al estiramiento:
Fe = k . ΔX [1]
Y por otro lado, debemos aplicar ahora la ley de Newton, ΣF = m a |
|
|
|
Pero hay un problema: las fuerzas no son codireccionales, son oblicuas entre sí. Debemos hacer una descomposición. Voy a elegir (a propósito) un SR con una coordenada horizontal (la misma dirección de la aceleración) y la otra vertical. El peso no hay que descomponerlo, coincide con la dirección vertical. Sí, en cambio, Fe. |
|
|
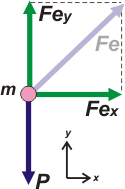 |
Y ahora aplicamos la Segunda Ley por separado para cada uno de los ejes. Empecemos con la dirección horizontal
ΣFx = m ax
hay una sola fuerza en esa dirección; y ax no es otra que la aceleración del vagón
Fex = m a
Ahora vamos con la dirección vertical
ΣFy = m ay
Fey – P = 0
Fey = m g
|
|
|
|
| Pareciera que no ganamos demasiado... pero tratemos de ver si Fex y Fey, no estan por casualidad, realacionados de alguna manera. |
|
|
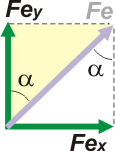 |
Mirá el triangulito que quedó formado y que sombreé en gris. Es rectángulo, no cabe duda. El ángulo α no es otro que el ángulo de inclinación de la cuerda. Tx y Ty son los catetos de ese triángulo y T es la hipotenusa. Entonces...
Fex = Fe . sen α
Fey = Fe . cos α
Si metemos esta información en las ecuaciones de Newton tal como las habíamos dejado, quedan: |
|
|
|
Fe . sen α = m a [2]
Fe . cos α = m g [3]
ahora dividimos miembro a miembro esas dos ecuaciones y mirá lo que queda
tg α = a / g
|
|
|
|
|
|
Ya tenemos una respuesta, nos falta el estiramiento. Tomemos la Ley de Hooke que describe el comportamiento del resorte y la reemplazamos en cualquiera de las ecuaciones [2] o [3], total, ya sabemos cuánto vale el ángulo alfa.
k . ΔX . sen α = m a [4]
k . ΔX . cos α = m g [5]
|
|
|
| |
ΔX = m a / k sen α y ΔX = m g / k cos α |
|
|
|
|
Ambas expresiones son equivalentes. Y ambas adolecen de la misma desprolijidad: no están expresadas en función de los datos del ejercicio en forma exclusiva... pero -ya te lo aclaré antes- podemos considerar dato a alfa ya que lo calculamos antes.
|
|
 |
| * Este interesante ejercicio me lo envió Ramiro Díaz Ortiz, que ya lo había resuelto utilizando ¡un sistema de referencia no-inercial! |
|
DESAFIO: ¿Puede el resorte inclinarse respecto de la vertical sin estirarse? |
|
Algunos reservados (no es que sean tímidos, callados).
Se permite su reproducción citando la fuente. Última actualización jul-07. Buenos Aires, Argentina.
|
|
|

