NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(Gravitación)
|
|

|
NMS 4.14 * - Europa es un satélite de Júpiter que tarda 3,55 días en recorrer su órbita, de radio medio 6,71 .108 m, en torno a dicho planeta. Otro satélite de Júpiter, Ganímedes, tiene un período orbital de 7,15 días. Calcula el radio medio de la órbita de Ganímedes.
Tenemos dos maneras de resolver este ejercicio: la formal, metodológica, parsimoniosa, segura, larga, detallada, plomaza, que voy a desarrollar a continuación, y la cortita y simpática que plantearía sólo para mí y para obtener el resultado rápidamente. La segunda te la cuento después.
Pero primero el esquema: |
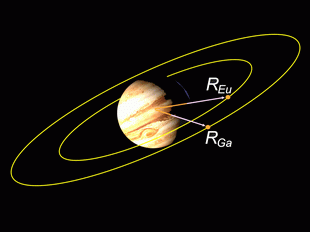 |
|
Está un poquito fuera de escala... pero igual sirve, no te olvides que es un esquema.
Muy bonito Júpiter orbitado por Europa a una distancia REu de su centro y por Ganímedes a una distancia RGa. Es obvio que Ganímedes orbita a mayor distancia, pero aunque no te dieses cuenta de eso, no es crucial para resolver el ejercicio.
Cada uno tardará un tiempo TEu y TGa en darle una vuelta completa respectivamente. |
|
|
|
Vamos desde cero. Sobre cada satélite actúa una única fuerza que es la fuerza gravitatoria, FG, de atracción con Júpiter (las fuerzas entre ambos satélites son despreciables respecto de la que les hace Júpiter). De esa fuerza habla tanto la segunda ley de la dinámica, como la ley de gravitación universal:
FG = mS . acS
FG = G . mS . MJ / RS²
El subíndice S denota "satélite" ya que las cosas ocurren igual para ambos. La fuerza de la que habla la 2da. ley y la ley de gravitación son la misma fuerza, de modo que puedo igualar las ecuaciones. En lugar de escribir aceleración centrípeta de cada satélite voy a usar alguna de sus expresiones equivalentes. Elijo alguna que hable del período,T, porque es uno de los datos del enunciado. Ésta, mirá, ac = 4π² . R /T²
mS . 4π² . RS / TS² = G . mS . MJ / RS²
La masa del satélite, mS, se puede cancelar, y RS es simultáneamente la distancia desde los centros de los cuerpos, el radio de órbita, la cuestión es que se pueden juntar. Para cada satélite tendremos:
REu³/TEu² = G . MJ / 4π²
RGa³/TGa² = G . MJ / 4π²
Los segundos miembros son idénticos, entonces podemos igualar los primeros:
REu³/TEu² = RGa³/TGa² [1]
En esta expresión la única incógnita es el radio de órbita de Ganímedes, el resto son datos del enunciado. Lo despejo y calculo:
RGa³ = REu³ . TGa² /TEu²
RGa³ = (6,71 .108 m)³ . (7,15 d)² / (3,55 d)²
No te olvides sacarle la raíz cúbica al resultado de esa cuenta. |
|
|
|
|
|
| |
|
|
La ecuación que te marqué [1] tiene nombre: se trata de la 3era. ley de Kepler, que dice que los cubos de los radios de órbita son proporcionales a los cuadrados de los períodos de rotación, para satélites de un cuerpo central.
Uno de los sistemas orbitales con los que trabajó Johannes Kepler para arribar a esa sorprendente conclusión fue, justamente, el sistema de Júpiter y sus cuatro satélites observables desde la Tierra con el telescopio de Galileo.
La forma sencilla de resolver este ejercicio consiste en partir nuestro razonamiento desde ahí, desde la ley de Kepler, y liquidarlo en un único renglón de álgebra. Es cierto que las leyes de Kepler no tienen la relevancia física de las de Newton, pero sí suficiente entidad como para arrancar desde ahí y que los docentes no te cuestionen el procedimiento. |
|
|
|
|
 |
| DESAFIO: ¿Cuánto valdrá el radio orbital de Calisto, que da una vuelta completa a Júpiter en 16,69 días? |
|
| Algunos derechos reservados.
Se permite tu reproducción recitando en la fuente. Última actualización jul-12. Buenos Aires, Argentina. |
|
|
|

