NO ME SALEN
EJERCICIOS RESUELTOS DE FÍSICA DEL CBC
(gravitación)
|
|

|
 |
NMS d4.07 - Newton llegó a la Teoría de Gravitación
Universal suponiendo que la Luna “caía” sobre
la Tierra. Sus cálculos corroboraron la idea fundando
de este modo la teoría. Intente seguir los
pasos que condujeron a esta idea con la ayuda
de los siguientes dibujos |
|
Este ejercicio es interesantísimo. Y sencillísimo. Si lo seguís paso a paso, vas a arribar a un conocimiento fundamental.
|
|
|
|
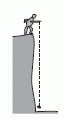 |
Lo que porpone el enunciado es que sigas la secuencia de dibujos que aparecen y los vayas analizando... y enlazando sucesivamente.
El primero te muestra un chabón dejando caer verticalmente un objeto. Se trata de una caída libre común y silvestre. Ya lo viste en cinemática y a esta altura del partido no te cabe duda de que el cuerpo se mueve aceleradamente. Las ecuaciones del movimiento ya te son familiares: Δy = ½ g Δt² |
|
|
|
Y podrías calcular fácilmente que en el primer segundo de caída el cuerpo cae 4,9 m (tomando g = 9,8 m/s²) |
|
|
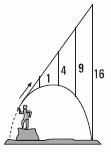 |
El segundo movimiento nos muestra un tiro oblicuo común y silvestre. Si el tiro resultara en una trayectoria rectilínea, con un MRU, que se pierde en el espacio podríamos dividirlo en tramos iguales, a intervalos de tiempos iguales. Bien, lo que te muestra el dibujo es que la curva real, resultante de un tiro oblicuo yace cada vez más abajo de la recta oblicua de la velocidad inicial.
¿Cuánto más abajo? La diferencia vertical crece al cuadrado de los tiempos de avance... |
|
|
|
| Si en 1 tiempo baja 1 metro, en 2 baja 4, en 3 baja 9, en 4 baja 16... y así. Esto lo más probable es que no lo hayas ejercitado como para poder verlo así durante tus prácticas de tiro oblicuo... pero podrías hacerlo... es súper fácil. |
|
|
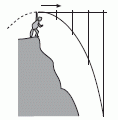 |
El tercer movimiento muestra un tiro horizontal desde la cima de una colina. La trayectoria del cuerpo es bien conocida por vos. Podés tratar de vincularlo con la imagen anterior... ya que dice exactamente lo mismo, pero más sencillo y obvio, porque la velocidad inicial es horizontal. |
|
|
|
| Fácilmente podrías calcular la "caída total medida desde la horizontal de partida" al cabo de 1 s, 2 s, etc. |
|
|
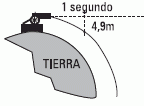 |
Este dibujo muestra exactamente lo mismo que el anterior, excepto por un cambio de escala. En este dibujo se muestra una porción del planeta Tierra, con su curvatura, su redondez. Pero el cambio de escala no implica ningún cambio cualitativo respecto de lo que viste en el dibujo anterior.
El gran cambio es que para tener un movimiento como éste la velocidad de partida debe ser mucho más grande de la que puede imprimir un lanzador humano. Por eso hay un cañon. |
|
|
|
| El dibujo te agrega un detalle que debés mantener presente en la argumentación. Al cabo de un segundo el proyectil habrá descendido (respecto de la recta inicial) unos 4,9 m, igual que en la caída libre del principio. |
|
|
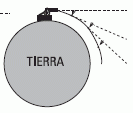 |
Acá viene la conclusión, la frutilla del postre. Supongamos que no hay aire que frene al proyectil. Entonces la velocidad que tiene al cabo de un segundo será igual que la que tenía a la salida del cañón, pero apuntaría más abajo.
A partir de ese instante, entonces, podemos repetir el argumento pensando que dentro de un segundo le pasará exactamente lo mismo que le pasó en el anterior. |
|
|
|
| Cuando vemos la secuencia completa nos demos cuenta que el proyectil dio una vuelta completa a la Tierra simplemente cayendo todo el tiempo. Cayendo a razón de 4,9 m por cada segundo de vuelo. |
|
|
| |
Caer y orbitar son básicamente el mismo fenómeno
pero en escalas diferentes. |
|
|
|
|
| Galileo Galilei llegó a esta misma conclusión y por idéntico razonamiento unos 50 años antes que Newton. |
|
|
Discusión: En este breve artículo tenés un razonamiento equivalente (aunque algo diferente) que lleva a la misma conclusión.
Desafío: Con respecto a la discusión anterior... ¿cuáles son los números que cambian si nos referimos al orbitar de la Luna? |
|
 |
| |
|
| |
| Algunos derechos reservados.
Este material didáctico no puede ser comercializado... Pero podés leerlo, memorizarlo, olvidarlo, imprimirlo, copiarlo, prestarlo, compartirlo, regalarlo, atesorarlo, y muchas cosas más. Última actualización may-13. Buenos Aires, Argentina. |
|
|
|

